题目内容

二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，若|ax2＋bx＋c|＝k(k≠0)有两个不相等的实数根，则k的取值范围是（     ）
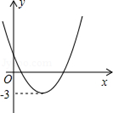
A．k＜－3B．k＞－3C．k＜3D．k＞3
D．

试题分析：∵当ax2+bx+c≥0，y=ax2+bx+c（a≠0）的图象在x轴上方，
∴此时y=|ax2+bx+c|=ax2+bx+c，
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c（a≠0）在x轴上方部分的图象，
∵当ax2+bx+c＜0时，y=ax2+bx+c（a≠0）的图象在x轴下方，
∴此时y=|ax2+bx+c|=﹣（ax2+bx+c）
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c（a≠0）在x轴下方部分与x轴对称的图象，
∵y=ax2+bx+c（a≠0）的顶点纵坐标是﹣3，
∴函数y=ax2+bx+c（a≠0）在x轴下方部分与x轴对称的图象的顶点纵坐标是3，
∴y=|ax2+bx+c|的图象如图，

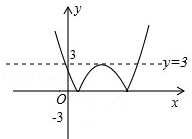
∵观察图象可得当k≠0时，
函数图象在直线y=3的上方时，纵坐标相同的点有两个，
函数图象在直线y=3上时，纵坐标相同的点有三个，
函数图象在直线y=3的下方时，纵坐标相同的点有四个，
∴若|ax2+bx+c|=k（k≠0）有两个不相等的实数根，
则函数图象应该在y=3的上边，
故k＞3．
故选D．
练习册系列答案
相关题目
如图，抛物线y=x2+mx+（m﹣1）与x轴交于点A（x1，0），B（x2，0），x1＜x2，与y轴交于点C（0，c），且满足x12+x22+x1x2=7．
（1）求抛物线的解析式；
（2）在抛物线上能不能找到一点P，使∠POC=∠PCO？若能，请求出点P的坐标；若不能，请说明理由．
已知关于x一元二次方程有两个不相等的实数根
（1）求k取值范围；
（2）当k最小的整数时，求抛物线的顶点坐标以及它与x轴的交点坐标；
（3）将（2）中求得的抛物线在x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分不变，得到一个新图象．请你画出这个新图象，并求出新图象与直线有三个不同公共点时m值．
在平面直角坐标系xOy中，已知二次函数的图象与x轴的正半轴交于A 、B两点（点A在点B的左侧），与y轴交于点C ．点A和点B间的距离为2， 若将二次函数的图象沿y轴向上平移3个单位时，则它恰好过原点，且与x轴两交点间的距离为4．
（1）求二次函数的表达式；
（2）在二次函数的图象的对称轴上是否存在一点P，使点P到B、C两点距离之差最大？若存在，求出点P坐标；若不存在，请说明理由；
（3）设二次函数的图象的顶点为D，在x轴上是否存在这样的点F，使得？若存在，求出点F的坐标；若不存在，请说明理由．
如图，直线y＝x＋m与抛物线y＝x2－2x＋l交于不同的两点M、N（点M在点N的左侧）．
(1)设抛物线的顶点为B，对称轴l与直线y＝x＋m的交点为C，连结BM、BN，若S△MBC＝S△NBC，求直线MN的解析式；
(2)在(1)条件下，已知点P(t，0)为x轴上的一个动点，
①若△PMN为直角三角形，求点P的坐标．
②若∠MPN>90°，则t的取值范围是     ．
已知抛物线经过点A（3，2），B（0，1）和点C．
（1）求抛物线的解析式；
（2）如图，若抛物线的顶点为P，点A关于对称轴的对称点为M，过M的直线交抛物线于另一点N（N在对称轴右边），交对称轴于F，若，求点F的坐标；
（3）在（2）的条件下，在y轴上是否存在点G，使△BMA与△MBG相似？若存在，求点G的坐标；若不存在，请说明理由．
如图，已知抛物线y＝x2＋bx＋c经过A(-1, 0)、B(4, 5)两点，过点B作BC⊥x轴，垂足为C．
（1）求抛物线的解析式；
（2）求tan∠ABO的值；
（3）点M是抛物线上的一个点，直线MN平行于y轴交直线AB于N，如果以M、N、B、C为顶点的四边形是平行四边形，求出点M的横坐标．
如图，矩形OABC在平面直角坐标系xoy中，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=4,OC=3，若抛物线的顶点在BC边上，且抛物线经过O、A两点，直线AC交抛物线于点D。
（1）求抛物线的解析式；
（2）求点D的坐标；
（3）若点M在抛物线上，点N在x轴上，是否存在以点A、D、M、N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由。
抛物线y =-2x2-3的顶点坐标是                 ；

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网