题目内容
二次函数y=x2+bx+c的图象如图所示．
（1）求此二次函数的解析式；
（2）求此二次函数图象与x轴的交点，当x满足什么条件时，函数值y＜0；
（3）把此抛物线向上平移多少个单位时，抛物线与x轴只有一个交点？并写出平移后的抛物线的解析式．
解：（1）由题意得：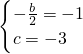
解得：
∴y=x2+2x-3
（2）当y=0时，x2+2x-3=0
得：x=-3，x=1
∴当-3＜x＜1时，y＜0
（3）y=x2+2x-3=（x+1）2-4
∴把此抛物线向上平移4个单位时，抛物线与x轴只有一个交点．
此时抛物线解析式为：y=（x+1）2即y=x2+2x+1
分析：（1）根据图象可知二次函数的对称轴是x=-1，并且经过点（0，-3），即常数项c=-3．即可求得函数解析式；
（2）求出函数与x轴的交点坐标即可根据图象求解；
（3）把函数化为顶点式y=a（x-h）2+k的形式，向上平移使抛物线与x轴只有一个交点，即把解析式中的k变成0即可．
点评：本题主要考查了二次函数对称轴顶点坐标的公式，以及函数与坐标轴交点坐标的求解方法．
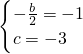
解得：
∴y=x2+2x-3
（2）当y=0时，x2+2x-3=0
得：x=-3，x=1
∴当-3＜x＜1时，y＜0
（3）y=x2+2x-3=（x+1）2-4
∴把此抛物线向上平移4个单位时，抛物线与x轴只有一个交点．
此时抛物线解析式为：y=（x+1）2即y=x2+2x+1
分析：（1）根据图象可知二次函数的对称轴是x=-1，并且经过点（0，-3），即常数项c=-3．即可求得函数解析式；
（2）求出函数与x轴的交点坐标即可根据图象求解；
（3）把函数化为顶点式y=a（x-h）2+k的形式，向上平移使抛物线与x轴只有一个交点，即把解析式中的k变成0即可．
点评：本题主要考查了二次函数对称轴顶点坐标的公式，以及函数与坐标轴交点坐标的求解方法．
练习册系列答案
相关题目