题目内容
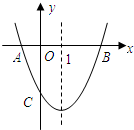 抛物线y1=ax2+bx+c交x轴于A、B两点,交y轴于点C,对称轴为直线x=1,且A、C两点的坐标分别为A(-1,0)、C(0,-3).
抛物线y1=ax2+bx+c交x轴于A、B两点,交y轴于点C,对称轴为直线x=1,且A、C两点的坐标分别为A(-1,0)、C(0,-3).(1)求抛物线y1=ax2+bx+c和直线BC:y2=mx+n的解析式;
(2)当y1•y2≥0时,直接写出x的取值范围.
分析:(1)根据抛物线的对称轴为直线x=1,且A点的坐标为A(-1,0),于是求出B点的坐标,利用待定系数法求出抛物线的解析式,已知B、C两点的坐标,即可求出y2=mx+n的解析式;
(2)根据图象找出抛物线y1=ax2+bx+c和直线BC:y2=mx+n图象在同一象限的部分的x的取值范围.
(2)根据图象找出抛物线y1=ax2+bx+c和直线BC:y2=mx+n图象在同一象限的部分的x的取值范围.
解答: 解:(1)∵抛物线y1=ax2+bx+c的对称轴为x=1,且A点的坐标为A(-1,0),
解:(1)∵抛物线y1=ax2+bx+c的对称轴为x=1,且A点的坐标为A(-1,0),
∵A、B两点关于x=1对称,
∴B点坐标为(3,1),
∵抛物线y1=ax2+bx+c经过A(-1,0)、B(3,0),C(0,-3),
∴
,
解得a=1,b=-2,c=-3,
∴抛物线的解析式为y1=x2-2x-3;
直线y2=mx+n经过B(3,0),C(0,-3),
∴
,
解得m=1,n=-3,
故直线解析式为y2=x-3;
 (2)连接BC,
(2)连接BC,
若y1•y2≥0,
则抛物线y1=ax2+bx+c和直线BC:y2=mx+n图象在同一象限,
由图象可以看出当x<-1时,y1>0,y2<0,
当x≥-1,y1•y2≥0,
即当y1•y2≥0时,x的取值范围为x≥-1.
 解:(1)∵抛物线y1=ax2+bx+c的对称轴为x=1,且A点的坐标为A(-1,0),
解:(1)∵抛物线y1=ax2+bx+c的对称轴为x=1,且A点的坐标为A(-1,0),∵A、B两点关于x=1对称,
∴B点坐标为(3,1),
∵抛物线y1=ax2+bx+c经过A(-1,0)、B(3,0),C(0,-3),
∴
|
解得a=1,b=-2,c=-3,
∴抛物线的解析式为y1=x2-2x-3;
直线y2=mx+n经过B(3,0),C(0,-3),
∴
|
解得m=1,n=-3,
故直线解析式为y2=x-3;
 (2)连接BC,
(2)连接BC,若y1•y2≥0,
则抛物线y1=ax2+bx+c和直线BC:y2=mx+n图象在同一象限,
由图象可以看出当x<-1时,y1>0,y2<0,
当x≥-1,y1•y2≥0,
即当y1•y2≥0时,x的取值范围为x≥-1.
点评:本题主要考查二次函数的综合题的知识点,解答本题的关键熟练利用抛物线的对称性求出B点的坐标,此题难度不大,第2问结合图形很容易解答.

练习册系列答案
相关题目
 已知点A(-1,n)(n>0)和点B(2,3)在抛物线y1=x2+bx+c上,点C(1,0)是x轴上一点,且CA+CB的值最小.
已知点A(-1,n)(n>0)和点B(2,3)在抛物线y1=x2+bx+c上,点C(1,0)是x轴上一点,且CA+CB的值最小.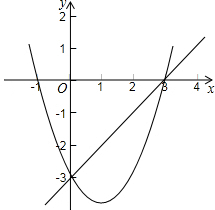 如图,抛物线y1=ax2+bx+c与直线y2=kx+h相交于(3,0)、(0,-3)两点,当y1>y2时,自变量x的取值范围是( )
如图,抛物线y1=ax2+bx+c与直线y2=kx+h相交于(3,0)、(0,-3)两点,当y1>y2时,自变量x的取值范围是( )
 如图,已知抛物线
如图,已知抛物线 如图,抛物线
如图,抛物线