ΧβΡΩΡΎ»ί
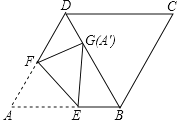
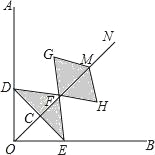
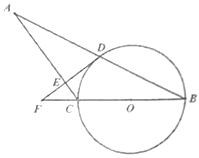
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§RtΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ΒψDΈΣAB±Ώ…œΒΡΕ·ΒψΘ®ΒψD≤Μ”κΒψAΘ§ΒψB÷ΊΚœΘ©Θ§ΙΐΒψDΉςEDΓΆCDΫΜ÷±œΏAC”ΎΒψEΘ§“―÷ΣΓœAΘΫ30ΓψΘ§ABΘΫ4cmΘ§‘ΎΒψD”…ΒψAΒΫΒψB‘ΥΕ·ΒΡΙΐ≥Χ÷–Θ§…ηADΘΫxcmΘ§AEΘΫycmΘ°
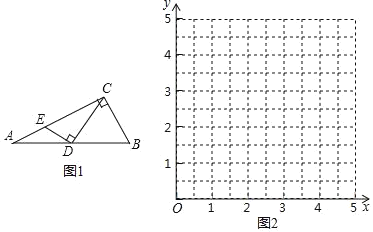
–ΓΕΪΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§Ε‘Κ· ΐyΥφΉ‘±δΝΩxΒΡ±δΜ·Εχ±δΜ·ΒΡΙφ¬…Ϋχ––ΝΥΧΫΨΩΘ°
œ¬Οφ «–ΓΕΪΒΡΧΫΨΩΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
Θ®1Θ©Ά®Ιΐ»ΓΒψΓΔΜ≠ΆΦΓΔ≤βΝΩΘ§ΒΟΒΫΝΥx”κyΒΡΦΗΉι÷ΒΘ§»γœ¬±μΘΚ
x/cm | Γ≠ |
| 1 |
| 2 |
| 3 |
| Γ≠ |
y/cm | Γ≠ | 0.4 | 0.8 | 1.0 | ΓΓ ΓΓ | 1.0 | 0 | 4.0 | Γ≠ |
Θ®ΥΒΟςΘΚ≤Ι»Ϊ±μΗώ ±œύΙΊ ΐ÷Β±ΘΝτ“ΜΈΜ–Γ ΐΘ©
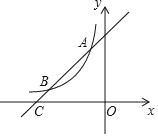
Θ®2Θ©‘Ύ»γΆΦ2ΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Οη≥ω“‘≤Ι»ΪΚσΒΡ±μ÷–ΗςΕ‘Ε‘”Π÷ΒΈΣΉχ±ξΒΡΒψΘ§Μ≠≥ωΗΟΚ· ΐΒΡΆΦœσΘΜ
Θ®3Θ©ΫαΚœΜ≠≥ωΒΡΚ· ΐΆΦœσΘ§ΫβΨωΈ ΧβΘΚΒ±AEΘΫ![]() AD ±Θ§AD
AD ±Θ§AD
ΓΨ¥πΑΗΓΩΘ®1Θ©1.2ΘΜΘ®2Θ©ΉςΆΦΦϊΫβΈωΘΜΘ®3Θ©2.4Μρ3.3.
ΓΨΫβΈωΓΩ
Θ®1Θ©Θ®2Θ©ΗυΨίΧβ“β≤βΝΩΓΔΉςΆΦΦ¥Ω…ΘΜ
Θ®3Θ©¬ζΉψAE![]() ADΧθΦΰΘ§ ΒΦ …œΩ…“‘ΉΣΜ·ΈΣ’ΐ±»άΐΚ· ΐy
ADΧθΦΰΘ§ ΒΦ …œΩ…“‘ΉΣΜ·ΈΣ’ΐ±»άΐΚ· ΐy![]() Θ°
Θ°
Θ®1Θ©ΗυΨίΧβ“βΘ§≤βΝΩΒΟ1.2Θ§ΓύΙ ¥πΑΗΈΣΘΚ1.2Θ°
Θ®2Θ©ΗυΨί“―÷Σ ΐΨίΘ§ΉςΆΦΒΟΘΚ
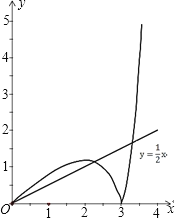
Θ®3Θ©Β±AE![]() AD ±Θ§y
AD ±Θ§y![]() Θ§‘ΎΘ®2Θ©÷–ΆΦœσΉςΆΦΘ§≤Δ≤βΝΩΝΫΗωΚ· ΐΆΦœσΫΜΒψΒΟΘΚ
Θ§‘ΎΘ®2Θ©÷–ΆΦœσΉςΆΦΘ§≤Δ≤βΝΩΝΫΗωΚ· ΐΆΦœσΫΜΒψΒΟΘΚ
AD=2.4Μρ3.3Θ°
Ι ¥πΑΗΈΣΘΚ2.4Μρ3.3Θ°