题目内容
定义:已知反比例函数 与
与 ,如果存在函数
,如果存在函数 (
( )则称函数
)则称函数 为这两个函数的中和函数.
为这两个函数的中和函数.
(1)试写出一对函数,使得它的中和函数为 ,并且其中一个函数满足:当
,并且其中一个函数满足:当 时,
时, 随
随 的增大而增大.
的增大而增大.
(2)
函数 和
和 的中和函数
的中和函数 的图象和函数
的图象和函数 的图象相交于两点,试求当
的图象相交于两点,试求当 的函数值大于
的函数值大于 的函数值时
的函数值时 的取值范围.
的取值范围.
【答案】
(1)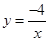 与
与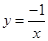 (答案不唯一,只要满足
(答案不唯一,只要满足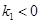 、
、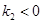 ,且
,且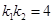 都可以);(2)
都可以);(2)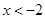 或
或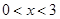 .
.
【解析】
试题分析:(1)首先根据中和函数的定义和已知的k值可以求出所求函数解析式的k的取值范围,由此即可求解,答案不唯一;
(2)由于函数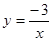 和
和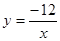 的中和函数
的中和函数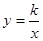 的图象和函数
的图象和函数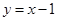 的图象相交于两点,由此可以求出k值,然后建立方程组,求出方程组的解得到交点坐标,再结合图象即可求解.
的图象相交于两点,由此可以求出k值,然后建立方程组,求出方程组的解得到交点坐标,再结合图象即可求解.
试题解析:(1)∵试写出一对函数,使得它的中和函数为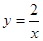 ,并且其中一个函数满足:当x<0时,y随x的增大而增大.∴答案不唯一,如
,并且其中一个函数满足:当x<0时,y随x的增大而增大.∴答案不唯一,如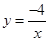 与
与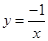 (只要满足
(只要满足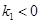 、
、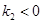 ,且
,且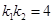 都可以);
都可以);
(2)∵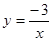 和
和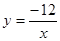 的中和函数
的中和函数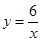 ,联立方程组
,联立方程组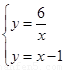 ,解得:
,解得: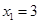 ,
,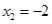 ,
解之得两个函数图象的交点坐标为(3,2)(-2,-3),结合图象得到当
,
解之得两个函数图象的交点坐标为(3,2)(-2,-3),结合图象得到当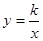 的函数值大于
的函数值大于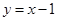 的函数值时x的取值范围是:
的函数值时x的取值范围是: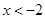 或
或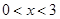 .
.
考点:1.反比例函数的性质;2.反比例函数的图象;3.新定义.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 与
与 ,如果存在函数
,如果存在函数 (k1k2>0)则称函数
(k1k2>0)则称函数 为这两个函数的中和函数.
为这两个函数的中和函数. ,并且其中一个函数满足:当x<0时,y随x的增大而增大.
,并且其中一个函数满足:当x<0时,y随x的增大而增大. 和
和 的中和函数
的中和函数 的图象和函数y=2x的图象相交于两点,试求当
的图象和函数y=2x的图象相交于两点,试求当 的函数值大于y=2x的函数值时x的取值范围.
的函数值大于y=2x的函数值时x的取值范围. 与
与 ,如果存在函数
,如果存在函数 (k1k2>0)则称函数
(k1k2>0)则称函数 为这两个函数的中和函数.
为这两个函数的中和函数. ,并且其中一个函数满足:当x<0时,y随x的增大而增大.
,并且其中一个函数满足:当x<0时,y随x的增大而增大. 和
和 的中和函数
的中和函数 的图象和函数y=2x的图象相交于两点,试求当
的图象和函数y=2x的图象相交于两点,试求当 的函数值大于y=2x的函数值时x的取值范围.
的函数值大于y=2x的函数值时x的取值范围.