题目内容
定义:已知反比例函数 与
与 ,如果存在函数
,如果存在函数 (k1k2>0)则称函数
(k1k2>0)则称函数 为这两个函数的中和函数.
为这两个函数的中和函数.(1)试写出一对函数,使得它的中和函数为
 ,并且其中一个函数满足:当x<0时,y随x的增大而增大.
,并且其中一个函数满足:当x<0时,y随x的增大而增大.(2)函数
 和
和 的中和函数
的中和函数 的图象和函数y=2x的图象相交于两点,试求当
的图象和函数y=2x的图象相交于两点,试求当 的函数值大于y=2x的函数值时x的取值范围.
的函数值大于y=2x的函数值时x的取值范围.
【答案】分析:(1)首先根据中和函数的定义和已知的k值可以求出所求函数解析式的k的取值范围,由此即可求解,答案不唯一;
(2)由于函数 和
和 的中和函数
的中和函数 的图象和函数y=2x的图象相交于两点,由此可以求出k值,然后建立方程组,求出方程组的解得到交点坐标,再结合图象即可求解.
的图象和函数y=2x的图象相交于两点,由此可以求出k值,然后建立方程组,求出方程组的解得到交点坐标,再结合图象即可求解.
解答:解:(1)∵试写出一对函数,使得它的中和函数为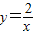 ,
,
并且其中一个函数满足:当x<0时,y随x的增大而增大.
∴答案不唯一,如 与
与 等;
等;
(2)∵ 和
和 的中和函数
的中和函数 ,
,
联立方程组 ,
,
解之得两个函数图象的交点坐标为( )(
)(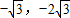 ),
),
结合图象得到当 的函数值大于y=2x的函数值时x的取值范围是
的函数值大于y=2x的函数值时x的取值范围是 或
或 .
.
点评:本题主要考查反比例函数图象和性质及图象上点的坐标特征,同时也利用了函数图象的交点坐标与函数解析式的关系.注意:反比例函数的增减性只指在同一象限内.
(2)由于函数
 和
和 的中和函数
的中和函数 的图象和函数y=2x的图象相交于两点,由此可以求出k值,然后建立方程组,求出方程组的解得到交点坐标,再结合图象即可求解.
的图象和函数y=2x的图象相交于两点,由此可以求出k值,然后建立方程组,求出方程组的解得到交点坐标,再结合图象即可求解.解答:解:(1)∵试写出一对函数,使得它的中和函数为
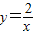 ,
,并且其中一个函数满足:当x<0时,y随x的增大而增大.
∴答案不唯一,如
 与
与 等;
等;(2)∵
 和
和 的中和函数
的中和函数 ,
,联立方程组
 ,
,解之得两个函数图象的交点坐标为(
 )(
)(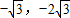 ),
),结合图象得到当
 的函数值大于y=2x的函数值时x的取值范围是
的函数值大于y=2x的函数值时x的取值范围是 或
或 .
.点评:本题主要考查反比例函数图象和性质及图象上点的坐标特征,同时也利用了函数图象的交点坐标与函数解析式的关系.注意:反比例函数的增减性只指在同一象限内.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 与
与 ,如果存在函数
,如果存在函数 (
( )则称函数
)则称函数 ,并且其中一个函数满足:当
,并且其中一个函数满足:当 时,
时, 随
随 的增大而增大.
的增大而增大. 和
和 的中和函数
的中和函数 的图象和函数
的图象和函数 的图象相交于两点,试求当
的图象相交于两点,试求当 与
与 ,如果存在函数
,如果存在函数 (k1k2>0)则称函数
(k1k2>0)则称函数 为这两个函数的中和函数.
为这两个函数的中和函数. ,并且其中一个函数满足:当x<0时,y随x的增大而增大.
,并且其中一个函数满足:当x<0时,y随x的增大而增大. 和
和 的中和函数
的中和函数 的图象和函数y=2x的图象相交于两点,试求当
的图象和函数y=2x的图象相交于两点,试求当 的函数值大于y=2x的函数值时x的取值范围.
的函数值大于y=2x的函数值时x的取值范围.