题目内容
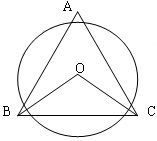
如图,在Rt△ABC中,已知∠ACB=90°,AC=1,BC=3,将△ABC绕着点A按逆时针方向旋转30°,使得点B与点B′重合,点C与点C′重合,则图中阴影部分的面积为 .


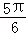
试题分析:先根据勾股定理得到AB=
 ,再根据扇形的面积公式计算出S扇形ABB′,由旋转的性质得到Rt△ADE≌Rt△ACB,于是S阴影部分=S△AC′B′+S扇形ABB′﹣S△ABC=S扇形ABB′,求出即可.
,再根据扇形的面积公式计算出S扇形ABB′,由旋转的性质得到Rt△ADE≌Rt△ACB,于是S阴影部分=S△AC′B′+S扇形ABB′﹣S△ABC=S扇形ABB′,求出即可.解:如图,∵∠ACB=90°,AC=1,BC=3,
∴AB=
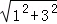 =
=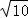 ,
,∴S扇形ABB′=
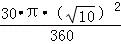 =
=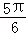 ,
,又∴Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,
∴Rt△ADE≌Rt△ACB,
∴S阴影部分=S△AC′B′+S扇形ABB′﹣S△ABC=S扇形ABB′=
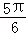

练习册系列答案
相关题目
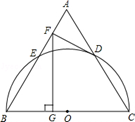


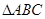 中,
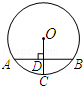
中,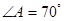 .⊙O截
.⊙O截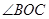 的度数为( )
的度数为( )