题目内容
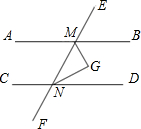 如图,如果AB∥CD,EF分别交AB、CD于M、N两点,∠BMN与∠DNM的平分线交于点G,那么∠G等于多少度?请说明理由.
如图,如果AB∥CD,EF分别交AB、CD于M、N两点,∠BMN与∠DNM的平分线交于点G,那么∠G等于多少度?请说明理由.
分析:由AB∥CD,根据两直线平行,同旁内角互补,即可求得∠BMN+∠DNM=180°,又由∠BMN与∠DNM的平分线交于点G,即可求得∠GMN+∠GNM=90°,然后由三角形内角和定理,求得∠G的度数.
解答:解:∠G=90°.
理由:∵AB∥CD,
∴∠BMN+∠DNM=180°,
∵∠BMN与∠DNM的平分线交于点G,
∴∠GMN=
∠BMN,∠GNM=
∠DNM,
∴∠GMN+∠GNM=90°,
∴∠G=180°-(∠GMN+∠GNM)=90°.
理由:∵AB∥CD,
∴∠BMN+∠DNM=180°,
∵∠BMN与∠DNM的平分线交于点G,
∴∠GMN=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GMN+∠GNM=90°,
∴∠G=180°-(∠GMN+∠GNM)=90°.
点评:此题考查了平行线的性质与三角形内角和定理,角平分线的定义.注意两直线平行,同旁内角互补.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
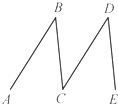 20、如图,如果AB∥CD,∠B=37°,∠D=37°,那么BC与DE平行吗?若平行,请说明你的理由.
20、如图,如果AB∥CD,∠B=37°,∠D=37°,那么BC与DE平行吗?若平行,请说明你的理由.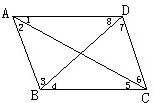 28、如图,如果AB∥CD,那么图中相等的内错角是( )
28、如图,如果AB∥CD,那么图中相等的内错角是( )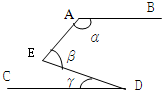
 如图,如果AB∥CD,∠ABE=30°,∠BEC=55°,∠ECD=
如图,如果AB∥CD,∠ABE=30°,∠BEC=55°,∠ECD=