题目内容
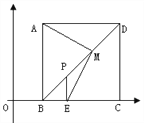
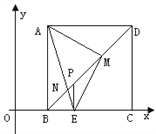
【题目】如图,直线AB交x轴于点B(4,0),交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°.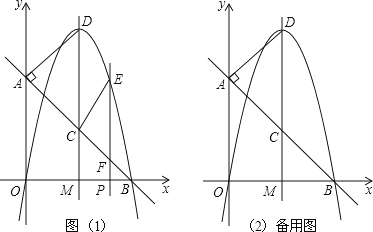
(1)直接写出直线AB的解析式;
(2)求点D的坐标;
(3)若点P是线段MB上的动点,过点P作x轴的垂线,交AB于点F,交过O、D、B三点的抛物线于点E,连接CE.是否存在点P,使△BPF与△FCE相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:设直线AB的解析式为y=kx+b,将A(0,4),B(4,0)两点坐标代入,
得 ![]() ,解得
,解得 ![]() ,所以,直线AB的解析式为y=﹣x+4;
,所以,直线AB的解析式为y=﹣x+4;
(2)
解:过D点作DG⊥y轴,垂足为G,
∵OA=OB=4,
∴△OAB为等腰直角三角形,
又∵AD⊥AB,
∴∠DAG=90°﹣∠OAB=45°,即△ADG为等腰直角三角形,
∴DG=AG=OG﹣OA=DM﹣OA=6﹣4=2,
∴D(2,6);
(3)
解:存在.
由抛物线过O(0,0),B(4,0)两点,设抛物线解析式为y=ax(x﹣4),
将D(2,6)代入,得a=﹣ ![]() ,所以,抛物线解析式为y=﹣
,所以,抛物线解析式为y=﹣ ![]() x(x﹣4),
x(x﹣4),
由(2)可知,∠PBF=45°,则∠CFE=∠BFP=45°,C(2,2),
设P(x,0),则MP=x﹣2,PB=4﹣x,
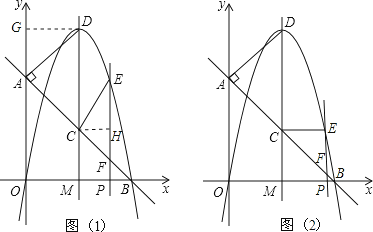
①当∠ECF=∠BPF=90°时(如图1),△BPF与△FCE相似,
过C点作CH⊥EF,此时,△CHE、△CHF、△PBF为等腰直角三角形,
则PE=PF+FH+EH=PB+2MP=4﹣x+2(x﹣2)=x,
将E(x,x)代入抛物线y=﹣ ![]() x(x﹣4)中,得x=﹣
x(x﹣4)中,得x=﹣ ![]() x(x﹣4),解得x=0或
x(x﹣4),解得x=0或 ![]() ,即P(
,即P( ![]() ,0),
,0),
②当∠CEF=∠BPF=90°时(如图2),此时,△CEF、△BPF为等腰直角三角形,
则PE=MC=2,将E(x,2)代入抛物线y=﹣ ![]() x(x﹣4)中,得2=﹣
x(x﹣4)中,得2=﹣ ![]() x(x﹣4),
x(x﹣4),
解得x= ![]() 或
或 ![]() ,即P(
,即P( ![]() ,0),
,0),
所以,P( ![]() ,0)或(
,0)或( ![]() ,0).
,0).
【解析】(1)根据A(0,4),B(4,0)两点坐标,可求直线AB的解析式;(2)作DG⊥y轴,垂足为G,由已知得OA=OB=4,△OAB为等腰直角三角形,而AD⊥AB,利用互余关系可知,△ADG为等腰直角三角形,则DG=AG=OG﹣OA=DM﹣OA=6﹣4=2,可求D点坐标;(3)存在.已知O(0,0),B(4,0),设抛物线的交点式,将D点坐标代入求抛物线解析式,由于对顶角∠CFE=∠BFP=45°,故当△BPF与△FCE相似时,分为:∠ECF=∠BPF=90°,∠CEF=∠BPF=90°两种情况,根据等腰直角三角形的性质求P点坐标.

【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元