题目内容
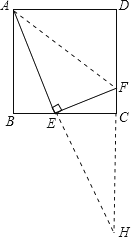
【题目】如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.
(1)求证:△ABE∽△ECF;
(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你的结论.
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECF;
(2)
证明:E是中点时,∠BAE=∠EAF,
理由如下:
连接AF,延长AE于DC的延长线相交于点H,
∵E为BC中点,
∴BE=CE,
∵AB∥DH,
∴∠B=∠ECH,
∵∠AEB=∠CEH,
∴△ABE≌△HCE,
∴AE=EH,
∵EF⊥AH,
∴△AFH是等腰三角形,
∴∠EAF=∠H,
∵AB∥DH,
∴∠H=∠BAE,
∴∠BAE=∠EAF,
∴当点E在BC中点位置时,∠BAE=∠EAF.
【解析】(1)有正方形的性质和已知条件证明∠BAE=∠FEC即可证明:△ABE∽△ECF;(2)连接AF,延长AE于DC的延长线相交于点H,当点E在BC中点位置时,通过证明三角形全等和等腰三角形的性质以及平行线的性质即可证明∠BAE=∠EAF.
【考点精析】利用正方形的性质和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】随着我国经济的高速发展,有着“经济晴雨表”之称的股市也得到迅速的发展,下表是今年上证指数某一周星期一至星期五的变化情况. (注:上周五收盘时上证指数为2616点,每一天收盘时指数与前一天相比,涨记为“+”,跌记为“-”)
星 期 | 一 | 二 | 三 | 四 | 五 |
指数的变化(与前一天比较) |
|
|
|
|
|
⑴ 请求出这一周星期五收盘时的上证指数是多少点?
⑵ 说出这一周每一天收盘时上证指数哪一天最高?哪一天最低?分别是多少点?