题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=2![]() ,BC=4
,BC=4![]() ,D、E分别是边AB、BC的中点,点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作EDFP,设点P的运动时间为t(秒).
,D、E分别是边AB、BC的中点,点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作EDFP,设点P的运动时间为t(秒).

(1)求AB长.
(2)当∠DPF=∠PFD时,求t的值.
(3)当点P在线段CD上时,设EDFP与△ABC重叠部分图形的面积为y(平方单位),求y与t之间的函数关系式.
(4)连结AF,当△AFD的面积与△PDE的面积相等时,直接写出t的值.
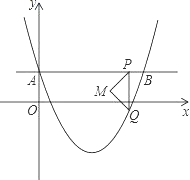
【答案】(1)10;(2)![]() .(3) y=
.(3) y=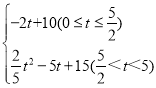 .(4) 0或
.(4) 0或![]() .
.
【解析】
试题分析:(1)在RT△ABC中利用勾股定理即可解决问题.
(2)如图1中,当∠DPF=∠PFD时,可以证明PE∥AB,PC=PD,由此即可解决问题.
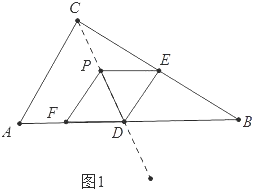
(3)分两种情形①当0≤t≤![]() 时,如图2中,作PM⊥DE存在为M,此时重叠部分面积就是平行四边形PEDF的面积,②当
时,如图2中,作PM⊥DE存在为M,此时重叠部分面积就是平行四边形PEDF的面积,②当![]() <t<5时,如图3中,此时y=S△PHD+S△PDE.
<t<5时,如图3中,此时y=S△PHD+S△PDE.
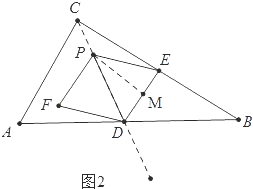
(4)两种情形①t=O时,△ADF与△PDE面积相等.②如图4中,当A、P、E共线时△ADF与△PDE面积相等,由DE∥AC得![]() ,求出PC即可.
,求出PC即可.
试题解析:(1)在△ABC中,∵∠ACB=90°,AC=2![]() ,BC=4
,BC=4![]() ,
,
∴AB=![]() .
.
(2)如图1中,
∵四边形PEDF是平行四边形,
∴PF∥DE,PE∥DF,
∴∠DPF=∠PDE,
∵∠ACB=90°,AD=DB,
∴CD=DB=DA=5,∵CE=EB,
∴DE⊥BC,∠CDE=∠EDB
∵∠DPF=∠PFD,
∴∠PED=∠BDE,
∴PE∥DB,∵CE=EB,
∴PC=PD=![]() ,
,
∴t=![]() .
.
(3)①当0≤t≤![]() 时,如图2中,
时,如图2中,
作PM⊥DE存在为M,
∵PM∥CE,
∴![]() ,
,
∴![]() ,
,
∴PM=![]() (5-t),
(5-t),
∴y=DEPM=![]()
![]() (5-t)=-2t+10.
(5-t)=-2t+10.
②当![]() <t<5时,如图3中,
<t<5时,如图3中,
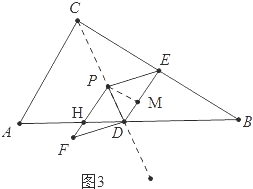
∵PH∥AC,
∴![]() ,
,
∴![]() ,
,
∴H=![]() (5-t),
(5-t),
∴y=S△PHD+S△PDE=![]() PHPM+
PHPM+![]() (-2t+10)=
(-2t+10)=![]() t2-5t+15,
t2-5t+15,
综上所述:y=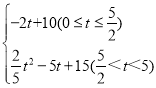 .
.
(4)①t=O时,△ADF与△PDE面积相等.
②如图4中,
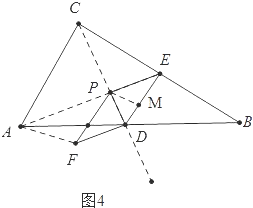
当A、P、E共线时,∵AE∥DF,
∴S△ADF=S△PDF=S△PED,
∵DE∥AC,
∴![]() ,
,
∴PC=![]() ,
,
∴t=![]() ,
,
∴t=0或![]() 时,△ADF与△PDE面积相等.
时,△ADF与△PDE面积相等.

 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分为100分)分成四类,并制作了如下的统计图表:
类别 | 成绩 | 频数 |
甲 | 60≤m<70 | 5 |
乙 | 70≤m<80 | a |
丙 | 80≤m<90 | 10 |
丁 | 90≤m≤100 | 5 |

根据图表信息,回答下列问题:
(1)该班共有学生________人;表中a=________;
(2)将丁类的五名学生分别记为A、B、C、D、E,现从中随机挑选两名学生参加学校的决赛,请借助树状图、列表或其他方式求B一定能参加决赛的概率.