题目内容
【题目】如图1,在锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,且BF=AC。求证:ED平分∠FEC。

【答案】证明见解析
【解析】分析:求出∠DBF=∠DAC,由AAS证明△BDF≌△ADC.得出对应边相等BD=AD,由等腰直角三角形的性质得出∠BAD=∠ABD=45°,证明A、B、D、E四点共圆,由圆周角定理得出∠BED=∠BAD=45°,得出∠CED=∠BED,即可得出结论.
本题解析:
∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=90°,∠AEB=∠FEC=90°,
∵∠DBF+∠C=90°,∠DAC+∠C=90°,
∴∠DBF=∠DAC,
在△BDF和△ADC中,
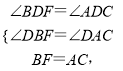
∴△BDF≌△ADC(AAS),
∴BD=AD,
∴∠BAD=∠ABD=45°,
∵∠AEB=∠ADB=90°,
∴A、B、D、E四点共圆,
∴∠BED=∠BAD=45°,
∴∠CED=90°-45°=45°=∠BED,
∴ED平分∠FEC。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




