��Ŀ����
����Ŀ��С���ڡ����������硱����������һ���⣺��ͼ1����֪��AOB=30�����߶�a�����������߳�Ϊa�ĵȱ������Ρ�COD��С���������ǣ���ͼ2����OΪԲ�ģ��߶�aΪ�뾶�������ֱ�OA��OB�ڵ�M��N���ڻ�MN����ȡһ��P���Ե�MΪԲ�ģ�MPΪ�뾶����������CD�ڵ�C��ͬ���Ե�NΪԲ�ģ�N PΪ�뾶����������CD�ڵ�D������CD������COD��������ĵȱ������Σ� 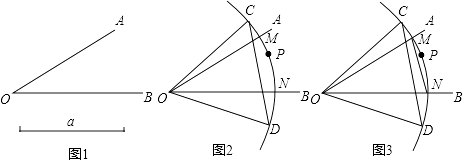
��1����д��С���������������ɣ�
��2���ڴ˻��������������²�����̽������ͼ3��������MN��MN�Ƿ�ƽ����CD��Ϊʲô��
��3����P��ʲôλ��ʱ��MN��CD������С������ͼ������ͼ1������ͼ�Σ���д������������ͼ�ۼ�����
���𰸡�
��1���⣺��ͼ2������OP��
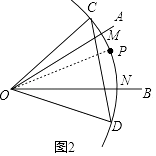
������ɵ� ![]() =
= ![]() ��
��
���COM=��POM�� ![]() =
= ![]() ��
��
���PON=��DON��
���POM+��PON=��COM+��DON=30�㣬
���COD=2��MON=60�㣬
���OCD�ǵȱ������Σ�
��2���⣺��һ����ֻ�е���COM=15�㣬CD��MN��
���ɣ��ߡ�COM=15�㣬��MON=30�㣬
���CON=45�㣬
�ߡ�C=60�㣬
���OEC=75�㣬
��ON=OM��
���ONM=��OMN=75�㣬
���OEC=��ONM��
��CD��MN
��3���⣺��P�� ![]() ���е�ʱ��MN��CD����ͼ3��ʾ��
���е�ʱ��MN��CD����ͼ3��ʾ��
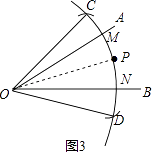
����������1����ͼ2������OP��������ɵ� ![]() =
= ![]() ��
�� ![]() =
= ![]() �����ǵõ���COM=��POM����PON=��DON������֪�����õ���COD=2��MON=60�㣬���ǵõ����ۣ���2�������������ҵõ���CON=45�㣬�õ���OEC=75�㣬���ݵ��������ε����ʵõ���ONM=��OMN=75�㣬��á�OEC=��ONM������ƽ���ߵ��ж��������ɵõ����ۣ���3����P��
�����ǵõ���COM=��POM����PON=��DON������֪�����õ���COD=2��MON=60�㣬���ǵõ����ۣ���2�������������ҵõ���CON=45�㣬�õ���OEC=75�㣬���ݵ��������ε����ʵõ���ONM=��OMN=75�㣬��á�OEC=��ONM������ƽ���ߵ��ж��������ɵõ����ۣ���3����P�� ![]() ���е�ʱ��MN��CD��������������ͼ�μ��ɣ�
���е�ʱ��MN��CD��������������ͼ�μ��ɣ�
�����㾫����ͨ���������ƽ���ߵ��ж������ʺ͵ȱ������ε��ж��������ɽǵ���Ȼ���������ϵ�����������õ�����ֱ��ƽ�У�λ�ù�ϵ������ƽ���ߵ��ж�����ƽ���ߣ�λ�ù�ϵ���õ��йؽ���Ȼ���������ϵ���Ľ�����ƽ���ߵ����ʣ������Ƕ���ȵ��������ǵȱ������Σ���һ���ǵ���60��ĵ����������ǵȱ������μ����Խ����⣮