题目内容
【题目】如图,已知:![]() 是
是![]() 的内接三角形,
的内接三角形,![]() 是
是![]() 延长线上的一点,连接
延长线上的一点,连接![]() ,且
,且![]() .
.
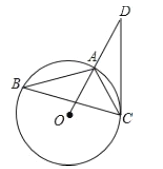
(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)直线![]() 与
与![]() 的位置关系是相切,理由见解析;(2)
的位置关系是相切,理由见解析;(2)![]()
【解析】
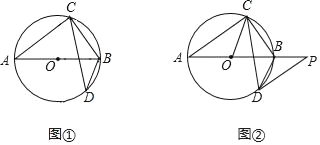
(1)连接OC,根据圆周角定理求出∠AOC,根据三角形内角和定理求出∠OCD,根据切线判定推出即可;
(2)连接OB,求出∠AOB=90°,根据等边三角形的性质和判定求出OA=6,根据勾股定理求出即可.

(1)解:直线![]() 与
与![]() 的位置关系是相切,
的位置关系是相切,
理由是:连接![]() ,
,
∵![]() 和
和![]() 分别是弧
分别是弧![]() 对的圆心角和圆周角,
对的圆心角和圆周角,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为半径,
为半径,
∴直线![]() 是
是![]() 的切线,
的切线,
即直线![]() 与
与![]() 的位置关系是相切.
的位置关系是相切.
(2)解:连接![]() ,
,
∵![]() 和
和![]() 分别是弧
分别是弧![]() 对的圆心角和圆周角,
对的圆心角和圆周角,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() .
.

练习册系列答案
相关题目