题目内容
【题目】问题情境
小明和小丽共同探究一道数学题:
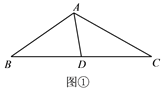
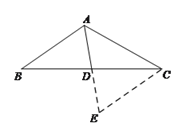
如图①,在△ABC中,点D是边BC的中点,∠BAD=65°,∠DAC=50°,AD=2,
求AC.
探索发现
小明的思路是:延长AD至点E,使DE=AD,构造全等三角形.
小丽的思路是:过点C作CE∥AB,交AD的延长线于点E,构造全等三角形.
选择小明、小丽其中一人的方法解决问题情境中的问题.
类比应用
如图②,在四边形ABCD中,对角线AC、BD相交于点O,点O是BD的中点,
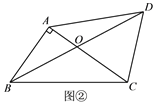
AB⊥AC.若∠CAD=45°,∠ADC=67.5°,AO=2,则BC的长为___________.
【答案】![]()
【解析】分析:探索发现:按照两个人的做题思路,作图,证明全等即可.
类比应用:参照探索发现的方法,进行求解即可.
详解:探索发现
小明的方法:
延长AD至点E,使DE=AD=2,如图.
∴AE=AD+DE=2+2=4.
∵点D是边BC的中点,
∴BD=CD.
∵∠ADB=∠EDC,
∴△ABD≌△ECD.
∴∠AEC=∠BAD=65°.
∴∠ACE=180°-∠EAC-∠AEC=180°-50°-65°=65°.
∴∠ACE=∠AEC.
∴AC=AE=4.
∴AC的长为4.
小丽的方法:
过点C作CE∥AB,交AD的延长线于点E,如图.
∴∠DCE =∠ABD,∠AEC=∠BAD=65°.
∴∠ACE=180°-∠EAC-∠AEC=180°-50°-65°=65°.
∴∠ACE=∠AEC.
∴AC=AE.
∵点D是边BC的中点,
∴BD=CD.
∴△ABD≌△ECD.
∴DE=AD=2.
∴AE=AD+DE=2+2=4.
∴AC=AE=4.
∴AC的长为4.
类比应用: 过点D作DE∥AB,交AD于点E,如图.
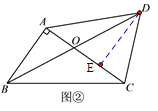
∴∠AED =∠DEC =∠BAC=90°,
∴∠ACD=180°-∠CAD-∠ADC=180°-45°-67.5°=67.5°.
∴∠ACD=∠ADC.
∴AC=AD.
∵点O是边BD的中点,
∴BO=OD.
∴△ABO≌△EDO.
∴AO=OE=2.
∴AE=DE=AB=4.
![]()
∴![]()
故答案为:![]() .
.