��Ŀ����
����Ŀ���������Ǻ��������¹�ʽ��sin����+�£�=sin��cos��+cos��sin�£�sin�������£�=sin��cos�©�cos��sin��
cos����+�£�=cos��cos�©�sin��sin�£�cos�������£�=cos��cos��+sin��sin��
tan����+�£�=![]() ��1��tan��tan�¡�0��
��1��tan��tan�¡�0��
tan�������£�=![]() ��1+tan��tan�¡�0��
��1+tan��tan�¡�0��
������Щ��ʽ���Խ�һЩ��������ǵ����Ǻ���ת��Ϊ����ǵ����Ǻ�������ֵ��
�磺tan105��=tan��45��+60�㣩=![]()
���������֪ʶ�������ѡ���ʵ��Ĺ�ʽ����������⣺
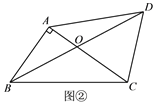
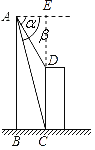
��ͼ������������AB��DC��ˮƽ����BCΪ24�ף��ӵ�A��õ�D�ĸ��Ǧ�=15�㣬��õ�C�ĸ��Ǧ�=75�㣬������CD�ĸ߶ȣ�

���𰸡�48![]() m
m
��������������������ȸ�����Ŀ�и����Ĺ�ʽ���tan75���tan15���ֵ����A��AE��CD��CD�ӳ�����E������Rt��AEC�������κ���ֵ�ó�CE��ֵ��Ȼ�����Rt��AED�������κ���ֵ�ó�DE�ij��ȣ�������CD=CE��DE�ó��𰸣�
����������⣺��tan75��=tan��30��+45����=![]() =
=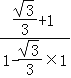 =2+
=2+![]() ��
��
tan15��=tan��45�㩁30����=![]() =2��
=2��![]() ��
��
��ͼ����A��AE��CD��CD�ӳ�����E�� ��Rt��AEC�У�AE=BC=24m����CAE=75����
��tan75��=![]() �� ��CE=AEtan75��=��48+24
�� ��CE=AEtan75��=��48+24![]() ��m��
��m��
��Rt��AED��tan��DAE=tan15��=![]() �� ��DE=AEtan15��=48��24
�� ��DE=AEtan15��=48��24![]() m��
m��
��CD=CE��DE=48![]() m��
m��
����������CD�ĸ߶���48![]() m��
m��

 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д�����Ŀ��������Զ�������п�ѡ����Ŀ֮һ������������ʦ��¼��ijͬѧ��һ��������Զ�ɼ������
�ɼ���m�� | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
�����й����������ݵ�˵������ȷ���ǣ�������
A.������2.3B.ƽ������2.4
C.�����2.5D.������0.01