题目内容
【题目】如图：直线AB经过点A（0，3）点B（ 
，0），点M在y轴上，⊙M经过点A、B，交x轴于另一点C． 
（1）求直线AB的解析式；
（2）求点M的坐标；
（3）点P是劣弧AC上一个动点，当P点运动时，问：线段PA，PB，PC有什么数量关系？并给出证明．
【答案】
（1）解：设直线AB的解析式为y=kx+b，
把点A（0，3）和点B（ 
，0）代入y+kx+b得到 
，
解得 
，
∴直线AB的解析式为y=﹣ x+3
（2）解：如图1中，连接BM．设AM=BM=r．
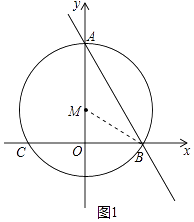
在Rt△BMO中，
∵OM2+OB2=BM2，OM=3﹣r，OB= ，
∴（3﹣r）2+（ ）2=r2，
∴r=2，
∴OM=3﹣2=1，
∴点M坐标为（0，1）
（3）解：结论：PB=PA+PC，理由如下：
如图2中，连接AC、在PB上截取PN=PC，连接CN．
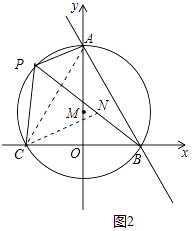
∵OM⊥BC，
∴OC=OB，
∴AC=AB，
∵tan∠ABO= 
= 
= ，
∴∠ABC=60°，
∴△ABC是等边三角形，
∴AC=CB，∠ACB=∠CAB=60°，
∴∠CPB=∠CAB=60°，∵PC=PN，
∴△PCN是等边三角形，
∴CP=CN，∠PCN=60°，
∴∠PCN=∠ACB=60°，
∴∠PCA=∠NCB，∵PC=CN，CA=CB，
∴△PCA≌△NCB，
∴PA=BN，
∵PB=PN+BN，PN=PC，BN=PA，
∴PB=PA+PC．
【解析】（1）设直线AB的解析式为y=kx+b，把点A（0，3）和点B（ ，0）代入y+kx+b得到 解方程组即可．（2）如图1中，连接BM．设AM=BM=r．在Rt△BMO中，由OM2+OB2=BM2 ， OM=3﹣r，OB= ，可得（3﹣r）2+（ ）2=r2 ， 解方程即可．（3）结论：PB=PA+PC，如图2中，连接AC、在PB上截取PN=PC，连接CN．首先证明△ACB，△PCN都是等边三角形，再证明△PCA≌△NCB，推出PA=BN，由此即可解决问题．
