ΧβΡΩΡΎ»ί
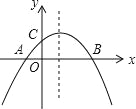
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=ax2+bx+2Θ®aΓΌ0Θ©”κx÷αΫΜ”ΎAΘ®4Θ§0Θ©ΓΔBΘ®©¹1Θ§0Θ©ΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘ§≤Δ–¥≥ωΤδΕ‘≥Τ÷αΘΜ
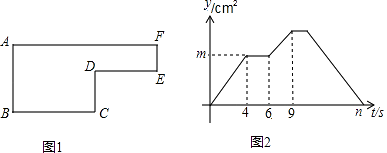
Θ®2Θ©Α―Θ®1Θ©÷–Υυ«σ≥ωΒΡ≈ΉΈοœΏΦ«ΈΣC1Θ§ΫΪC1œρ”“ΤΫ“ΤmΗωΒΞΈΜΒΟΒΫ≈ΉΈοœΏC2Θ§C1”κC2ΒΡ‘ΎΒΎ“ΜœσœόΫΜΒψΈΣMΘ§ΙΐΒψMΉςMGΓΆx÷α”ΎΒψGΘ§ΫΜœΏΕΈAC”ΎΒψHΘ§Ν§Ϋ”CMΘ§Β±ΓςCMHΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§«σ≈ΉΈοœΏœρ”“ΤΫ“ΤΒΡΨύάκmΚΆ¥Υ ±ΒψMΒΡΉχ±ξΘ°

ΓΨ¥πΑΗΓΩ(1)ΓΔy=©¹![]() x2+
x2+![]() x+2Θ§Ε‘≥Τ÷α «ΘΚ÷±œΏx=
x+2Θ§Ε‘≥Τ÷α «ΘΚ÷±œΏx=![]() ΘΜ(2)ΓΔm=1Θ§MΘ®2Θ§3Θ©.
ΘΜ(2)ΓΔm=1Θ§MΘ®2Θ§3Θ©.
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚ(1)ΓΔάϊ”ΟΫΜΒψ Ϋ«σΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘ§≤Δ≈δΖΫ«σΕ‘≥Τ÷αΘΜ(2)ΓΔœ»«σ÷±œΏACΒΡΫβΈω ΫΘ§ΗυΨίΗςΉ‘ΒΡΫβΈω Ϋ…η≥ωMΘ®xΘ§©¹![]() x2+
x2+![]() +2Θ©Θ§HΘ®xΘ§©¹
+2Θ©Θ§HΘ®xΘ§©¹![]() x+2Θ©Θ§”…ΆΦΒΟΓςCMHΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§CM=CHΘ§‘ρ”–GH+GM=4Θ§Ν– ΫΦΤΥψ«σ≥ωMΒΡΉχ±ξΘ§Α―MΒΡΉχ±ξ¥ζ»κΤΫ“ΤΚσΒΡΫβΈω ΫΩ…≤ΔΒΟ≥ωmΒΡ÷ΒΘ°
x+2Θ©Θ§”…ΆΦΒΟΓςCMHΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§CM=CHΘ§‘ρ”–GH+GM=4Θ§Ν– ΫΦΤΥψ«σ≥ωMΒΡΉχ±ξΘ§Α―MΒΡΉχ±ξ¥ζ»κΤΫ“ΤΚσΒΡΫβΈω ΫΩ…≤ΔΒΟ≥ωmΒΡ÷ΒΘ°
‘ΧβΫβΈωΘΚ(1)ΓΔΒ±x=0 ±Θ§y=ax2+bx+2=2Θ§ Γύ≈ΉΈοœΏΨ≠ΙΐΘ®0Θ§2Θ©Θ§
ΓΏ≈ΉΈοœΏy=ax2+bx+2Θ®aΓΌ0Θ©”κx÷αΫΜ”ΎAΘ®4Θ§0Θ©ΓΔBΘ®©¹1Θ§0Θ©ΝΫΒψΘ§
…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=aΘ®x©¹4Θ©Θ®x+1Θ©Θ§ Α―Θ®0Θ§2Θ©¥ζ»κΒΟΘΚ2=aΘ®0©¹4Θ©Θ®0+1Θ©Θ§ a=©¹![]() Θ§
Θ§
Γύy=©¹![]() Θ®x©¹4Θ©Θ®x+1Θ©=©¹
Θ®x©¹4Θ©Θ®x+1Θ©=©¹![]() x2+
x2+![]() +2=©¹
+2=©¹![]() Θ®x©¹
Θ®x©¹![]() Θ©2+
Θ©2+![]() Θ§
Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=©¹![]() x2+
x2+![]() +2Θ§Ε‘≥Τ÷α «ΘΚ÷±œΏx=
+2Θ§Ε‘≥Τ÷α «ΘΚ÷±œΏx=![]() ΘΜ
ΘΜ
(2)ΓΔ…η÷±œΏACΒΡΫβΈω ΫΈΣΘΚy=kx+bΘ§ Α―AΘ®4Θ§0Θ©ΓΔCΘ®0Θ§2Θ©¥ζ»κΒΟΘΚ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ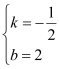 Θ§
Θ§
Γύ÷±œΏACΒΡΫβΈω ΫΈΣΘΚy=©¹![]() x+2Θ§ …ηMΘ®xΘ§©¹
x+2Θ§ …ηMΘ®xΘ§©¹![]() x2+
x2+![]() +2Θ©Θ§HΘ®xΘ§©¹
+2Θ©Θ§HΘ®xΘ§©¹![]() x+2Θ©Θ§
x+2Θ©Θ§
ΓΏΓςCMHΈΣΒ»―ϋ»ΐΫ«–ΈΘ§ ΓύCM=CHΘ§ ΓύC «MH¥Ι÷±ΤΫΖ÷œΏ…œΒΡΒψΘ§ ΓύGH+GM=4Θ§
‘ρ©¹![]() x2+
x2+![]() +2+Θ®©¹
+2+Θ®©¹![]() x+2Θ©=4Θ§ ΫβΒΟΘΚx1=0Θ®…αΘ©Θ§x2=2Θ§ ΓύMΘ®2Θ§3Θ©Θ§
x+2Θ©=4Θ§ ΫβΒΟΘΚx1=0Θ®…αΘ©Θ§x2=2Θ§ ΓύMΘ®2Θ§3Θ©Θ§
…ηΤΫ“ΤΚσΒΡ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚy=©¹![]() Θ®x©¹
Θ®x©¹![]() ©¹mΘ©2+
©¹mΘ©2+![]() Θ§ Α―MΘ®2Θ§3Θ©¥ζ»κΒΟΘΚm=1Θ°
Θ§ Α―MΘ®2Θ§3Θ©¥ζ»κΒΟΘΚm=1Θ°