题目内容
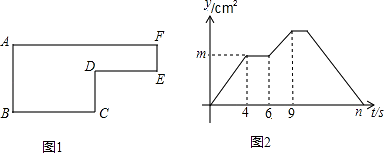
【题目】已知动点P以2cm/s的速度沿图1所示的边框从B→C→D→E→F→A的路径运动,记△ABP的面积为t(cm2),y与运动时间t(s)的关系如图2所示.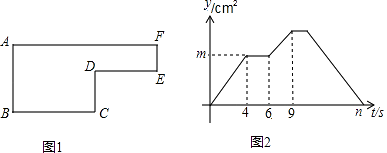
若AB=6cm,请回答下列问题:
(1)求图1中BC、CD的长及边框所围成图形的面积;
(2)求图2中m、n的值.
【答案】
(1)
解:由图2可知从B→C运动时间为4s,
∴BC=2×4=8cm,
同理CD=2×(6﹣4)=8cm,
∴边框围成图形面积=AF×AB﹣CD×DE=14×6﹣4×6=60cm2
(2)
解:m=S△ABC= ![]() ×AB×BC=24,
×AB×BC=24,
n=(BC+CD+DE+EF+FA)÷2=17.
【解析】(1)根据路程=速度×时间,即可解决问题.(2)由图象可知m的值就是△ABC面积,n的值就是运动的总时间,由此即可解决.
【考点精析】解答此题的关键在于理解函数的图象的相关知识,掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.

练习册系列答案
相关题目