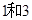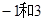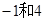题目内容
把方程x2－10x－11＝0化为(x＋m)2＝n的形式，结果为
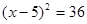
把常数项-11移项后，再在等式的两边同时加上一次项系数-10的一半的平方．
解：由原方程移项，得
x2-10x=11，
等式的两边同时加上一次项系数-10的一半的平方，得
x2-10x+52=11+52，
配方程，得
（x-5）2=36；
故答案是：（x-5）2=36．
考查了解一元二次方程--配方法．配方法的一般步骤：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
解：由原方程移项，得
x2-10x=11，
等式的两边同时加上一次项系数-10的一半的平方，得
x2-10x+52=11+52，
配方程，得
（x-5）2=36；
故答案是：（x-5）2=36．
考查了解一元二次方程--配方法．配方法的一般步骤：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
练习册系列答案
阅读快车系列答案
相关题目
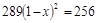
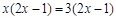
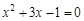
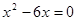小题2: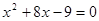
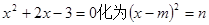的形式，指出
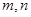分别是(▲)．
