题目内容
在平面直角坐标系中,有一个矩形ABCD,四个顶点的坐标分别为:A(4,0)、B(4,2)、C(8,2)、D(8,0),并且有两个动点P和Q.P从原点O出发,沿x轴正方向运动;Q从A点出发,沿折线A-B-C-D方向在矩形的边上运动,且两点的运动速度均为每秒2个单位.当Q到达D点时,P也随之停止.设运动的时间为x.(1)分别求出当x=1和x=3时,对应的△OPQ的面积;
(2)设△OPQ的面积为y,分别求出不同时段,y关于x的函数解析式,注明自变量的取值范围.并求出在整个运动过程中,△OPQ的面积的最大值;
(3)在P、Q运动过程中,是否存在两个时刻x1和x2,使得构成相应的△OP1Q1和△OP2Q2相似?若存在,直接写出这两个时刻,并证明两个三角形相似;若不存在,请说明理由.

分析:(1)根据面积公式即可求出答案;
(2)在运动过程中看P、Q的位置,根据面积公式计算即可;
(3)利用勾股定理求出线段长,根据三边对应成比例,两三角形相似即可得出结论.
(2)在运动过程中看P、Q的位置,根据面积公式计算即可;
(3)利用勾股定理求出线段长,根据三边对应成比例,两三角形相似即可得出结论.
解答:(1)解:当x=1时,面积为:S=
×(4-2)×2=2,
当x=3时,面积为S=
×(3×2)×2=6,
答:当x=1时,△OPQ的面积是2,当x=3时,△OPQ的面积是6.
(2)当0≤x≤1时,y1=
•2x•2x=2x2,
∴,y1=2x2,
同法可求:
当1≤x≤3时,y2=2x;
当3≤x≤4时,y3=-2x2+8x);
当x=3时,面积的最大值是6,
答:y1=2x2(0≤x≤1);y2=2x(1≤x≤3);y3=-2x2+8x(3≤x≤4).在整个运动过程中,△OPQ的面积的最大值是6.
(3)当x1=1,x2=2时,△OP1Q1和△OP2Q2相似.
因为OP1=2,P1Q1=2
,OQ1=2
;OP2=4,P2Q2=2
,OQ2=2
所以:
=
=
,
所以△OP1Q1和△OP2Q2相似.
| 1 |
| 2 |
当x=3时,面积为S=
| 1 |
| 2 |
答:当x=1时,△OPQ的面积是2,当x=3时,△OPQ的面积是6.
(2)当0≤x≤1时,y1=
| 1 |
| 2 |
∴,y1=2x2,
同法可求:
当1≤x≤3时,y2=2x;
当3≤x≤4时,y3=-2x2+8x);
当x=3时,面积的最大值是6,
答:y1=2x2(0≤x≤1);y2=2x(1≤x≤3);y3=-2x2+8x(3≤x≤4).在整个运动过程中,△OPQ的面积的最大值是6.
(3)当x1=1,x2=2时,△OP1Q1和△OP2Q2相似.
因为OP1=2,P1Q1=2
| 2 |
| 5 |
| 2 |
| 10 |
所以:
| OP1 |
| Q2P2 |
| P1Q1 |
| P2O |
| OQ1 |
| Q2O |
所以△OP1Q1和△OP2Q2相似.
点评:本题主要考查了二次函数,矩形的性质,相似三角形的性质和判定,三角形的面积,勾股定理等知识点,综合运用性质进行计算是解此题的关键.本题综合性比较强,有一定的难度.

练习册系列答案
相关题目
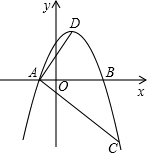 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=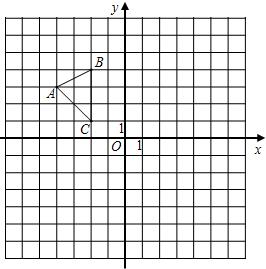 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.