Question

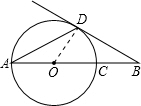
如图，AD是⊙O的弦，AB经过圆心O，交⊙O于点C，∠DAB=∠B=30°．
（1）求证：直线BD与⊙O相切；
（2）若AC=10，求BD的长．

Answer 1

（1）证明：连接OD，
∵OA=OD，∠DAB=∠B=30°，
∴∠ODA=∠DAB=∠B=30°，
又∠BOD为△AOD的外角，
∴∠BOD=∠DAB+∠ODA=60°，
∴∠ODB=180°-∠BOD-∠B=180°-60°-30°=90°，即OD⊥BD，
∴直线BD与⊙O相切；

（2）∵AC为⊙O的直径，AC=10，
∴OA=OC=OD=5，
又在Rt△OBD中，∠B=30°，
∴OD=

1

2

OB，
∴OB=2OD=10，
则由勾股定理得，BD=

OB2-OD2

=

102-52

=5

3

．