题目内容
如图,小区的一角有一块形状为等腰梯形的空地,为了美化小区,社区居委会计
划在空地上建一个四边形的水池,水池的四个顶点 恰好是梯形各边的中点,则水池的形状
一定是【 】

划在空地上建一个四边形的水池,水池的四个顶点 恰好是梯形各边的中点,则水池的形状
一定是【 】

| A.等腰梯形 | B.矩形 | C.菱形 | D.正方形 |
C
考点:
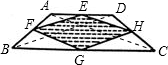
分析:根据梯形的对角线相等,所以连接各边中点的四边形是菱形.
解答:解:如图,连接对角线AC、BD.
∵点E为AD的中点,点F为AB的中点,
∴EF=BD/2,
同理可得:GH=BD/2,FG=AC/2,EH=AC/2,
又等腰梯形的对角线相等,即AC=BD,
∴EF=GH=FG=EH,
所以连接各边中点的四边形是菱形.
故选C.
点评:本题考查连接四边形各边中点得到的四边形与原四边形对角线的关系:原四边形对角线相等,得到的四边形是菱形;原四边形对角线互相垂直,得到的四边形是矩形;原四边形对角线既相等又垂直,得到的四边形是正方形;原四边形对角线既不相等又不垂直,得到的四边形是平行四边形.需要熟练掌握.

分析:根据梯形的对角线相等,所以连接各边中点的四边形是菱形.
解答:解:如图,连接对角线AC、BD.
∵点E为AD的中点,点F为AB的中点,
∴EF=BD/2,
同理可得:GH=BD/2,FG=AC/2,EH=AC/2,
又等腰梯形的对角线相等,即AC=BD,
∴EF=GH=FG=EH,
所以连接各边中点的四边形是菱形.
故选C.
点评:本题考查连接四边形各边中点得到的四边形与原四边形对角线的关系:原四边形对角线相等,得到的四边形是菱形;原四边形对角线互相垂直,得到的四边形是矩形;原四边形对角线既相等又垂直,得到的四边形是正方形;原四边形对角线既不相等又不垂直,得到的四边形是平行四边形.需要熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 AD⊥BC,垂足为D,AE∥BC, DE∥AB.
AD⊥BC,垂足为D,AE∥BC, DE∥AB.




 、①②都错
、①②都错 中,
中,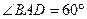 ,
, ,则菱形
,则菱形
