题目内容
【题目】综合题。
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为
②猜想线段AD,BE之间的数量关系为: , 并证明你的猜想.
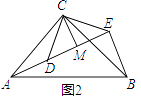
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM 为△DCE中DE边上的高,连接BE,请求出∠AEB的度数及线段CM,AE,BE 之间的数量关系.
【答案】
(1)60°;AD=BE
(2)
解:∠AEB=90°,AE﹣BE=2CM,
证明:∵△DCE是等腰直角三角形,CM是中线,
∴CM=DM=EM= ![]() DE,
DE,
在△ACD和△BCE中,
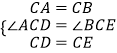 ,
,
∴△ACD≌△BCE,
∴∠CDA=∠CEB,
∵∠CDA=135°,
∴∠AEB=135°﹣45°=90°,
∴BE=AD,
∴AE﹣AD=DE=2CM,
∴AE﹣BE=2CM.
【解析】解:(1)①∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,即∠ACD=∠BCE,
在△ACD和△BCE中,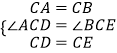 ,
,
∴△ACD≌△BCE,
∴∠CEB=∠CDA=120°,
∴∠AEB=60°,
所以答案是:60°;②AD=BE,
证明:∵△ACD≌△BCE,
∴AD=BE,
所以答案是:AD=BE;

练习册系列答案
相关题目


