Question

【题目】如图所示，已知BE⊥AC于E，CF⊥AB于F，BE、CF相交于点D，若BF=CE．求证：AD平分∠BAC．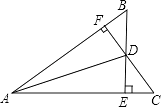

Answer 1

【答案】证明：∵BE⊥AC，CF⊥AB，
∴∠BFD=∠CED=90°，
在△BFD和△CED中

∴△BFD≌△CED（AAS），
∴DF=DE，
∵BE⊥AC，CF⊥AB，
∴AD平分∠BAC
【解析】根据垂直定义求出∠BFD=∠CED=90°，根据AAS推出△BFD≌△CED，根据全等三角形的性质推出DF=DE，根据角平分线性质求出即可．
【考点精析】根据题目的已知条件，利用角平分线的性质定理的相关知识可以得到问题的答案，需要掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上．