题目内容
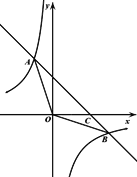
【题目】某地上年度电价为0.8元/度，年用电量为1亿度，本年度计划将电价调至0.55～0.75元/度之间，经测算，若电价调至x元/度，则本年度新增用电量y(亿度)与(x－0.4)成反比例．又知当x＝0.65时，y＝0.8.
(1)求y与x之间的函数解析式；
(2)若每度电的成本价为0.3元，则电价调至多少时，本年度电力部门的收益将比上年度增加20%？[收益＝用电量×(实际电价－成本价)]
【答案】(1) y＝
；(2) 当电价调至0.6元/度时，本年度电力部门的收益将比上年度增加20%.
【解析】
（1）因为本年度新增用电是y（亿度）与（x﹣0.4）成反比例关系，所以y
，根据当每度电价为0.65元时，新增用电是0.8亿度可确定k的值；
（2）设当电价为x元时，本年度电力部门的收益将比上年度增加20%，根据某地上年度电价为0.8元/度，全年用电1亿度，每度电成本0.3元，可列方程求解．
（1）∵本年度新增用电是y（亿度）与（x﹣0.4）成反比例关系，∴y．
∵当每度电价为0.65元时，新增用电是0.8亿度，∴0.8
，解得：k=0.2，∴y
；
（2）设当电价为x元时，本年度电力部门的收益将比上年度增加20%，根据题意得：
（0.8﹣0.3）（1+20%）=（
1）（x﹣0.3）
解得：x=0.6或x=0.5＜0.55（舍去）．
答：当电价为0.6元时，本年度电力部门的收益将比上年度增加20%．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】某商店购进一种商品，每件商品进价30元．试销中发现这种商品每天的销售量y（件）
与每件销售价x（元）的关系数据如下：
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
（1）已知y与x满足一次函数关系，根据上表，求出y与x之间的关系式（不写出自变量x的取值范围）；
（2）如果商店销售这种商品，每天要获得150元利润，那么每件商品的销售价应定为多少元？
（3）设该商店每天销售这种商品所获利润为w（元），求出w与x之间的关系式，并求出每件商品销售价定为多少元时利润最大？
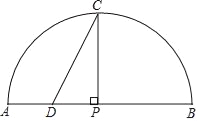
【题目】24如图，P是弧AB所对弦AB上一动点，过点P作PC⊥AB交弧AB于点C，取AP中点D，连接CD．已知AB＝6cm，设A，P两点间的距离为xcm，C．D两点间的距离为ycm．（当点P与点A重合时，y的值为0；当点P与点B重合时，y的值为3）
小凡根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小凡的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.2 |
| 3.2 | 3.4 | 3.3 | 3 |
（2）建立平面直角坐标系，描出补全后的表中各对对应值为坐标的点，画出该函数的图象；
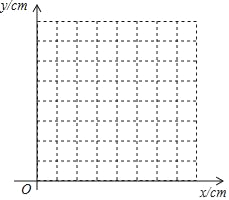
（3）结合所画出的函数图象，解决问题：当∠C＝30°时，AP的长度约为 cm．
