Question

【题目】如图，在矩形ABCD中，AB=3，AD=4，将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′，则点B经过的路径与BA，AC′，C′B′所围成封闭图形的面积是多少？（结果保留π）．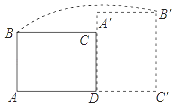

Answer 1

【答案】解：如图，连接BD与B′D，

点B经过的路径与BA，AC′，C′B′所围成封闭图形的面积是：
S扇形BDB′+S矩形ABCD= π×52+3×4= +12
【解析】根据点B经过的路径与BA，AC′，C′B′所围成封闭图形的面积是=S扇形BDB′+S矩形ABCD求解即可．
【考点精析】通过灵活运用矩形的性质和旋转的性质，掌握矩形的四个角都是直角，矩形的对角线相等；①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了即可以解答此题．