题目内容
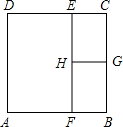 如图,E、F分别在矩形ABCD的边CD、AB上,EF⊥AB,G、H分别是BC、EF的中点,EH>HG,除矩形EFBC外,图中4个矩形都彼此相似,若BC=1,则AB等于( )
如图,E、F分别在矩形ABCD的边CD、AB上,EF⊥AB,G、H分别是BC、EF的中点,EH>HG,除矩形EFBC外,图中4个矩形都彼此相似,若BC=1,则AB等于( )A、
| ||||
B、1+
| ||||
C、
| ||||
D、1+
|
分析:根据条件矩形ABCD∽矩形EHGC,根据相似多边形对应边的比相等,即可求解.
解答:解:GC=
BC=0.5.设AB=CD=x,CE=y.则DE=x-y.
∵矩形ABCD∽矩形EHGC.
∴
=
,即
=
(1)
∵矩形ABCD∽矩形ADEF.
∴
=
,即
=
(2)
由(1)(2)解得:x=
.
故选C.
| 1 |
| 2 |
∵矩形ABCD∽矩形EHGC.
∴
| AB |
| GC |
| BC |
| HG |
| x |
| 0.5 |
| 1 |
| y |
∵矩形ABCD∽矩形ADEF.
∴
| AD |
| AB |
| DE |
| AD |
| 1 |
| x |
| x-y |
| 1 |
由(1)(2)解得:x=
| ||
| 2 |
故选C.
点评:本题主要考查了相似多边形的对应边的比相等,注意分清对应边是解决本题的关键.

练习册系列答案
相关题目
![]()
![]() 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 在第一象限内的图象经过点D、E,且 .
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 在第一象限内的图象经过点D、E,且 .
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩
| |
 |
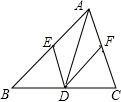 如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.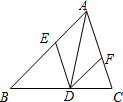 如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB. (定值),半径为
(定值),半径为 (定值),分别在图一、二中
(定值),分别在图一、二中 ,则按图二作出的矩
,则按图二作出的矩
 B.
B. C.
C. D.
D.