题目内容
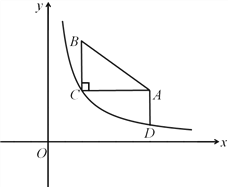
【题目】如图,在平面直角坐标系中,已知Rt△ABC中,∠C=90°,AC=4,BC=3,点A(6,5),B(2,8),反比例函数y![]() 过点C,过点A作AD∥y轴交双曲线于点D.
过点C,过点A作AD∥y轴交双曲线于点D.
(1)求反比例函数y![]() 的解析式;
的解析式;
(2)动点P在y轴正半轴运动,当线段PC与线段PD的差最大时,求P点的坐标;
(3)将Rt△ABC沿直线CO方向平移,使点C移动到点O,求线段AB扫过的面积.
【答案】(1)y=![]() (x>0);(2)26.
(x>0);(2)26.
【解析】分析:(1)根据平行关系确定出C的坐标,然后利用待定系数法求出函数的解析式,并根据图像表示出取值范围;
(2)根据题意判断出:当P、C、D三点共线时,线段PC与线段PD的差最大,求出D点的坐标,利用待定系数法,由C、D的坐标求解即可;
(3)根据平移的性质得到对应点的位置,利用分割法求出图形的面积即可.
详解:(1)设C(x,y)
由于AC∥x轴,BC∥x轴
得x=2,y=5即 C(2.5)
将C点代入y=![]() 得 k=10
得 k=10
则反比例函数为 y=![]() (x>0)
(x>0)
(2)当P、C、D三点共线时,线段PC与线段PD的差最大
设 D(6,a)
代入y=![]() 得a=
得a=![]() 所以D(6,
所以D(6,![]() )
)
设直线CD为y=kx+b, P(0,c)
将C(2.5),D(6,![]() )带入得
)带入得
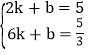
解得: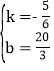
∴y=-![]() x+
x+![]()
将P(0,c)代入得c=![]()
即P(0,![]() )
)
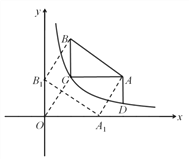
(3)如图所示
由题意可得点C移到点O;点B移到点B1(0,3);点A移到点A1 (4,0)
∴四边形B B1 OC,四边形A A1 OC与四边形B B1 A1 A都是平行四边形
在五边形B B1 OA1 A中有
S△ABC + SB B1 OC + SA A1 OC = S△O B1 A1 + SB B1 A1 A
∴![]() ×3×4+3×2+4×5 =
×3×4+3×2+4×5 =![]() ×3×4 + SB B1 A1 A
×3×4 + SB B1 A1 A
SB B1 A1 A = 26
即线段AB扫过的面积为26.