题目内容
(2012•高淳县一模)如图,将边长为a的正方形OABC绕顶点O按顺时针方向旋转角α(0°<α<45°),得到正方形OA1B1C1.设边B1C1与OC的 延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.
延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.
(1)求证:△OC1M≌△OA1E;
(2)试说明:△OMN的边MN上的高为定值;
(3)△MNB1的周长p是否发生变化?若发生变化,试说明理由;若不发生变化,请给予证明,并求出p的值.
 延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.
延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.(1)求证:△OC1M≌△OA1E;
(2)试说明:△OMN的边MN上的高为定值;
(3)△MNB1的周长p是否发生变化?若发生变化,试说明理由;若不发生变化,请给予证明,并求出p的值.
分析:(1)根据同角的余角相等可得∠A1OE=∠C1OM,然后利用“角边角”证明两三角形全等;
(2)根据(1)中全等三角形对应边相等可得OE=OM,再利用“边角边”证明△EON和△MON全等,根据全等三角形对应边上的高相等可得:△OMN的边MN上的高等于OA1的长度,是定值;
(3)根据全等三角形对应边相等可得MN=EN,A1E=C1M,然后推出△MNB1的周长p等于A1B1+B1C1,再根据旋转变换不改变图形的形状与大小,所以p=2a.
(2)根据(1)中全等三角形对应边相等可得OE=OM,再利用“边角边”证明△EON和△MON全等,根据全等三角形对应边上的高相等可得:△OMN的边MN上的高等于OA1的长度,是定值;
(3)根据全等三角形对应边相等可得MN=EN,A1E=C1M,然后推出△MNB1的周长p等于A1B1+B1C1,再根据旋转变换不改变图形的形状与大小,所以p=2a.
解答:(1)证明:∵正方形OABC,
∴∠A1OE+∠A1OM=∠C1OM+∠A1OM=90°,
∴∠A1OE=∠C1OM,
在△OC1M和△OA1E中,
,
∴△OC1M≌△OA1E(ASA);
(2)解:∵△OC1M≌△OA1E(已证),
∴OE=OM,
在△EON和△MON中,
,
∴△EON≌△MON(SAS),
∴EN=MN,
∴△OMN的边MN上的高等于△OEN边EN上的高,即OA1的长a,为定值;
(3)p不会发生变化,是定值2a.
理由如下:根据(1)(2),△OC1M≌△OA1E,△EON≌△MON,
∴MN=EN,A1E=C1M,
∴△MNB1的周长p=MN+NB1+MB1,
=EN+NB1+MB1,
=EB1+MB1,
=A1E+A1B1+MB1,
=C1M+A1B1+MB1,
=A1B1+B1C1,
∵正方形OABC的边长为a,
∴A1B1=B1C1=a,
∴p=2a,是定值.
∴∠A1OE+∠A1OM=∠C1OM+∠A1OM=90°,

∴∠A1OE=∠C1OM,
在△OC1M和△OA1E中,
|
∴△OC1M≌△OA1E(ASA);
(2)解:∵△OC1M≌△OA1E(已证),
∴OE=OM,
在△EON和△MON中,
|
∴△EON≌△MON(SAS),
∴EN=MN,
∴△OMN的边MN上的高等于△OEN边EN上的高,即OA1的长a,为定值;
(3)p不会发生变化,是定值2a.
理由如下:根据(1)(2),△OC1M≌△OA1E,△EON≌△MON,
∴MN=EN,A1E=C1M,
∴△MNB1的周长p=MN+NB1+MB1,
=EN+NB1+MB1,
=EB1+MB1,
=A1E+A1B1+MB1,
=C1M+A1B1+MB1,
=A1B1+B1C1,
∵正方形OABC的边长为a,
∴A1B1=B1C1=a,
∴p=2a,是定值.
点评:本题考查了旋转的性质,正方形的性质,全等三角形的判定与性质,是综合题,难度较大,把所求的值利用全等三角形转化为正方形的边长,从而得到定值是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目

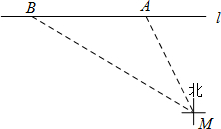 (2012•高淳县一模)《中华人民共和国道路交通管理条理》规定:“小汽车在城市街道公路上的行驶速度不得超过70km/h(即19.44m/s)”.如图所示,已知测速站M到街道公路l的距离为90m,一辆小汽车在街道公路l上由东向西行驶,测得此车从点A行驶到点B所用的时间为6s,并测得A在M的北偏西27°方向上,B在M的北偏西60°方向上.求出此车从A到B的平均速度,并判断此车是否超过限速.
(2012•高淳县一模)《中华人民共和国道路交通管理条理》规定:“小汽车在城市街道公路上的行驶速度不得超过70km/h(即19.44m/s)”.如图所示,已知测速站M到街道公路l的距离为90m,一辆小汽车在街道公路l上由东向西行驶,测得此车从点A行驶到点B所用的时间为6s,并测得A在M的北偏西27°方向上,B在M的北偏西60°方向上.求出此车从A到B的平均速度,并判断此车是否超过限速.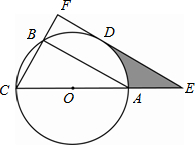 (2012•高淳县一模)已知△ABC内接于⊙O,AC是⊙O的直径,D是
(2012•高淳县一模)已知△ABC内接于⊙O,AC是⊙O的直径,D是