题目内容
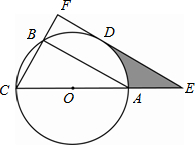 (2012•高淳县一模)已知△ABC内接于⊙O,AC是⊙O的直径,D是
(2012•高淳县一模)已知△ABC内接于⊙O,AC是⊙O的直径,D是 | AB |
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若CF=6,∠ACB=60°,求阴影部分的面积.
分析:(1)直线EF与圆O相切,理由为:连接OD,由AC为圆O的直径,根据直径所对的圆周角为直角可得出∠CBA为直角,再由CF垂直于FE,得到∠F为直角,根据同位角相等两直线平行可得出AB与EF平行,再由D为
的中点,利用垂径定理的逆定理得到OD垂直于AB,可得出∠AMO为直角,根据两直线平行同位角相等可得出∠ODE为直角,则EF为圆O的切线;
(2)在直角三角形CFE中,由CF的长,及∠E为30°,利用30°所对的直角边等于斜边的一半求出CE的长,再利用勾股定理求出EF的长,在直角三角形ODE中,由∠E为30°,利用30°所对的直角边等于斜边的一半得到OE=2OD,又OE=OA+AE,可得出AE=OA=OC,由CE的长求出半径OA的长,及OE的长,又OD垂直于EF,CF垂直于EF,得到一对直角相等,再由一对公共角相等,可得出三角形ODE与三角形CFE相似,根据相似得比例,将各自的值代入求出DE的长,再由∠E为30°求出∠DOE为60°,然后由阴影部分的面积=三角形ODE的面积-扇形OAD的面积,利用三角形的面积公式及扇形的面积公式计算即可得到阴影部分的面积.
 |
| AB |
(2)在直角三角形CFE中,由CF的长,及∠E为30°,利用30°所对的直角边等于斜边的一半求出CE的长,再利用勾股定理求出EF的长,在直角三角形ODE中,由∠E为30°,利用30°所对的直角边等于斜边的一半得到OE=2OD,又OE=OA+AE,可得出AE=OA=OC,由CE的长求出半径OA的长,及OE的长,又OD垂直于EF,CF垂直于EF,得到一对直角相等,再由一对公共角相等,可得出三角形ODE与三角形CFE相似,根据相似得比例,将各自的值代入求出DE的长,再由∠E为30°求出∠DOE为60°,然后由阴影部分的面积=三角形ODE的面积-扇形OAD的面积,利用三角形的面积公式及扇形的面积公式计算即可得到阴影部分的面积.
解答: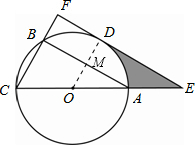 解:(1)直线EF与圆O相切,理由为:
解:(1)直线EF与圆O相切,理由为:
连接OD,如图所示:
∵AC为圆O的直径,∴∠CBA=90°,
又∵∠F=90°,
∴∠CBA=∠F=90°,
∴AB∥EF,
∴∠AMO=∠EDO,
又∵D为
的中点,
∴
=
,
∴OD⊥AB,
∴∠AMO=90°,
∴∠EDO=90°,
则EF为圆O的切线;
(2)在Rt△AEF中,∠ACB=60°,∴∠E=30°,
又∵CF=6,
∴CE=2CF=12,
根据勾股定理得:EF=
=6
,
在Rt△ODE中,∠E=30°,
∴OD=
OE,又OA=
OE,
∴OA=AE=OC=
CE=4,OE=8,
又∵∠ODE=∠F=90°,∠E=∠E,
∴△ODE∽△CFE,
∴
=
,即
=
,
解得:DE=4
,
又∵Rt△ODE中,∠E=30°,
∴∠DOE=60°,
则S阴影=S△ODE-S扇形OAD=
×4×4
-
=8
-
.
 解:(1)直线EF与圆O相切,理由为:
解:(1)直线EF与圆O相切,理由为:连接OD,如图所示:
∵AC为圆O的直径,∴∠CBA=90°,
又∵∠F=90°,
∴∠CBA=∠F=90°,
∴AB∥EF,
∴∠AMO=∠EDO,
又∵D为
 |
| AB |
∴
 |
| BD |
 |
| AD |
∴OD⊥AB,
∴∠AMO=90°,
∴∠EDO=90°,
则EF为圆O的切线;
(2)在Rt△AEF中,∠ACB=60°,∴∠E=30°,
又∵CF=6,
∴CE=2CF=12,
根据勾股定理得:EF=
| CE2-CF2 |
| 3 |
在Rt△ODE中,∠E=30°,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=AE=OC=
| 1 |
| 3 |
又∵∠ODE=∠F=90°,∠E=∠E,
∴△ODE∽△CFE,
∴
| OD |
| FC |
| DE |
| EF |
| 4 |
| 6 |
| DE | ||
6
|
解得:DE=4
| 3 |
又∵Rt△ODE中,∠E=30°,
∴∠DOE=60°,
则S阴影=S△ODE-S扇形OAD=
| 1 |
| 2 |
| 3 |
| 60•π•42 |
| 360 |
| 3 |
| 8π |
| 3 |
点评:此题考查了切线的性质,圆周角定理,平行线的判定与性质,相似三角形的判定与性质,含30°角直角三角形的性质,勾股定理,垂径定理的逆定理,以及扇形面积的求法,熟练掌握性质与定理是解本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目

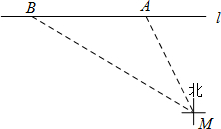 (2012•高淳县一模)《中华人民共和国道路交通管理条理》规定:“小汽车在城市街道公路上的行驶速度不得超过70km/h(即19.44m/s)”.如图所示,已知测速站M到街道公路l的距离为90m,一辆小汽车在街道公路l上由东向西行驶,测得此车从点A行驶到点B所用的时间为6s,并测得A在M的北偏西27°方向上,B在M的北偏西60°方向上.求出此车从A到B的平均速度,并判断此车是否超过限速.
(2012•高淳县一模)《中华人民共和国道路交通管理条理》规定:“小汽车在城市街道公路上的行驶速度不得超过70km/h(即19.44m/s)”.如图所示,已知测速站M到街道公路l的距离为90m,一辆小汽车在街道公路l上由东向西行驶,测得此车从点A行驶到点B所用的时间为6s,并测得A在M的北偏西27°方向上,B在M的北偏西60°方向上.求出此车从A到B的平均速度,并判断此车是否超过限速. 延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.
延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.