题目内容
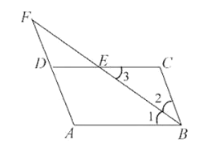
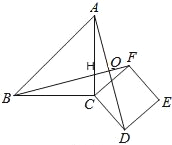
【题目】问题情境:如图1,△ABC为等腰直角三角形,∠ACB=90°,F是AC边上的一个动点(点F与A,C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF,AD.
探究展示:(1)①猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;
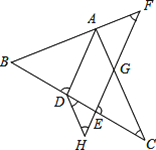
②将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度α,得到如图2的情形,图2中BF交AC于点H,交AD于点O,请你判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
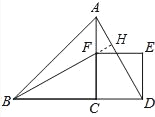
变式练习:(2)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90°,正方形CDEF改为矩形CDEF,如图3,且AC=4,BC=3,CD=![]() ,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,请判断线段BF、AD所在直线的位置关系,并证明你的判断.
,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,请判断线段BF、AD所在直线的位置关系,并证明你的判断.

【答案】(1)①结论:BF=AD,BF⊥AD;②BF=AD,BF⊥AD仍然成立,证明见解析;(2)结论:BF⊥AD,证明见解析.
【解析】试题分析:(1)①证△BCF≌△ACD推出∠CAD=∠FBC,BF=AD,即可得出结论;
②证△BCF≌△ACD推出∠CAD=∠FBC,BF=AD,即可得出结论;
(2)证△BCF∽△ACD,推出∠CBF=∠CAD,再根据∠BHC=∠AHO,∠CBH+∠BHC=90°从而得∠CAD+∠AHO=90°,继而得到∠AOH=90°,得到BF⊥AD.
试题解析:(1)①结论:BF=AD,BF⊥AD;
理由:如图,延长BF交AD于H,
∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∵四边形CDEF是正方形,
∴CD=CF,∠FCD=90°,
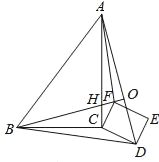
∴∠BCF=∠ACD,
在△BCF和△ACD中,
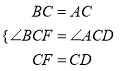 ,
,
∴△BCF≌△ACD(SAS),
∴BF=AD,∠CBF=∠CAD,
又∵∠BFC=∠AFH,∠CBF+∠BFC=90°,
∴∠CAD+∠AFH=90°,
∴∠AHF=90°,
∴BF⊥AD;
∴BF=AD,BF⊥AD;
②BF=AD,BF⊥AD仍然成立,
如图,
∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,
∵四边形CDEF是正方形,
∴CD=CF,∠FCD=90°,
∴∠ACB+∠ACF=∠FCD+∠ACF,
即∠BCF=∠ACD,
在△BCF和△ACD中,
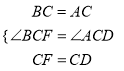 ,
,
∴△BCF≌△ACD(SAS),
∴BF=AD,∠CBF=∠CAD,
又∵∠BHC=∠AHO,∠CBH+∠BHC=90°,
∴∠CAD+∠AHO=90°,
∴∠AOH=90°,
∴BF⊥AD;
(2)结论:BF⊥AD.
如图,
∵四边形CDEF是矩形,
∴∠FCD=90°,
又∵∠ACB=90°,
∴∠ACB=∠FCD
∴∠ACB+∠ACF=∠FCD+∠ACF,
即∠BCF=∠ACD,
∵AC=4,BC=3,CD=![]() ,CF=1,
,CF=1,
∴![]() ,
,
∴△BCF∽△ACD,
∴∠CBF=∠CAD,
又∵∠BHC=∠AHO,∠CBH+∠BHC=90°
∴∠CAD+∠AHO=90°,
∴∠AOH=90°,
∴BF⊥AD.

【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
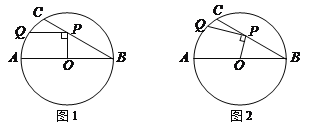
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
【题目】某商场计划用3 800元购进节能灯120只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?