题目内容
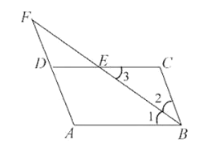
【题目】如图,在四边形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]()
(1)写出![]() 对由条件
对由条件![]() 推出的相等或互补的角
推出的相等或互补的角
(2)![]() 与
与![]() 相等吗?为什么?
相等吗?为什么?
(3)证明:![]()
请在下面的括号内,填上推理的根据,并完成下面的证明:
![]() ( ① )
( ① )
![]() (已证),
(已证),![]() ,( ② )
,( ② )
又![]() (角平分线的定义)
(角平分线的定义)
![]() ( ③ )
( ③ )
【答案】(1) ∠F=∠2,∠C=∠CDF,∠A+∠ABC=180°或∠C+∠ADC=180°;(2)相等,理由见解析;(3) 两直线平行,内错角相等;等量代换;内错角相等,两直线平行
【解析】
(1)依据平行线的性质,即可得出相等或互补的角(答案不唯一);
(2)依据对顶角相等以及等量代换,即可得出∠3与∠F相等.
(3)依据平行线的性质以及角平分线的定义,即可得到∠1=∠3,进而判定DC∥AB.
(1)∵AD∥CB,
∴∠F=∠2,∠C=∠CDF,∠A+∠ABC=180°或∠C+∠ADC=180°;
(2)∠3与∠F相等.理由:
∵∠DEF=∠F,∠3=∠DEF,
∴∠3=∠F.
(3)证明:∵AD∥BC,∴∠2=∠F.(①两直线平行,内错角相等);
∵∠3=∠F(已证),
∴∠2=∠3,(②等量代换);
又∵∠1=∠2(角平分线的定义),
∴∠1=∠3,
∴DC∥AB(③内错角相等,两直线平行).

练习册系列答案
相关题目







