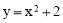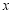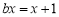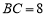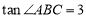题目内容
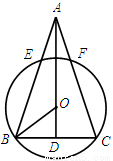
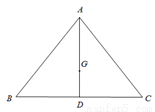
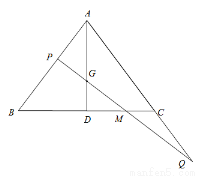
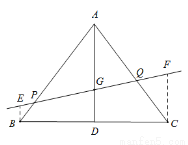
如图,已知在△ABC中,AB=AC,BC比AB大3,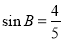 ,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
(1)求AG的长;
(2)当∠APQ=90º时,直线PG与边BC相交于点M.求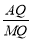 的值;
的值;
(3)当点Q在边AC上时,设BP=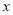 ,AQ=
,AQ=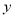 ,求
,求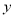 关于
关于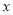 的函数解析式,并写出它的定义域.[
的函数解析式,并写出它的定义域.[
(1)AG=8;(2)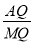 =
=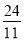 ;(3)
;(3)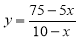
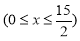 .
.
【解析】
试题分析:(1)根据已知条件和重心的性质得出BD=DC=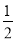 BC,AD⊥BC,再根据sinB=
BC,AD⊥BC,再根据sinB=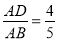 ,求出AB、BC、AD的值,从而求出AG的长;
,求出AB、BC、AD的值,从而求出AG的长;
(2)根据∠GMD+∠MGD=90°和∠GMD+∠B=90°,得出∠MGD=∠B,再根据特殊角的三角函数值求出DM、CM=CD-DM的值,在△ABC中,根据AA求出△QCM∽△QGA,即可求出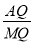 的值;
的值;
(3)过点B作BE∥AD,过点C作CF∥AD,分别交直线PQ于点E、F,则BE∥AD∥CF,得出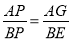 ,求出BE的值,同理可得出CF的值,最后根据BD=CD,求出EG=FG,即可得出CE+BE=2GD,从而得出求y关于x的函数解析式并得出它的定义域.
,求出BE的值,同理可得出CF的值,最后根据BD=CD,求出EG=FG,即可得出CE+BE=2GD,从而得出求y关于x的函数解析式并得出它的定义域.
试题解析:
(1)在△ABC中,∵AB=AC,点G是△ABC的重心,
∴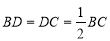 ,AD⊥BC.
,AD⊥BC.
在Rt△ADB中,∵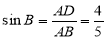 ,∴
,∴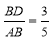 .
.
∵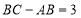 , ∴AB=15,BC=18.
, ∴AB=15,BC=18.
∴AD=12.
∵G是△ABC的重心,∴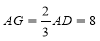 .
.
(2)在Rt△MDG,∵∠GMD+∠MGD=90°,
同理:在Rt△MPB中,∠GMD+∠B=90°,
∴∠MGD=∠B.
∴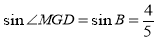 ,
,
在Rt△MDG中,∵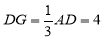 ,
,
∴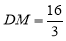 ,∴
,∴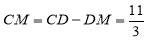
在△ABC中,∵AB=AC,AD⊥BC,∴ .
.
∵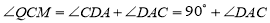 ,
,
又∵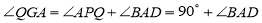 ,
,
∴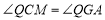 ,
,
又∵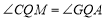 ,
,
∴△QCM∽△QGA.
∴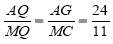 .
.
(3)过点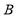 作
作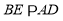 ,过点
,过点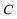 作
作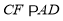 ,分别交直线
,分别交直线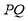 于点E、F,则
于点E、F,则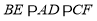 .
.
∵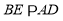 ,∴
,∴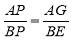 ,即
,即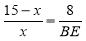 ,
,
∴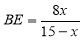
同理可得: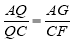 ,即
,即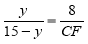 ,
,
∴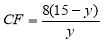 .
.
∵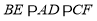 ,
, 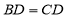 ,∴
,∴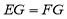 .
.
∴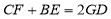 ,即
,即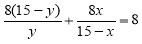 .
.
∴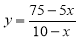 ,
,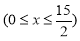 .
.
考点:相似形综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案