Question

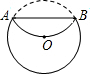如图，将半径为4cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长度为

 

cm．

Answer 1

分析：先过点O作OC⊥AB，垂足为C，连接OA，由题意求得OC，由勾股定理求得AC，再由垂径定理求得AB的值即可．

解答：解：如图，过点O作OC⊥AB，垂足为C，连接OA，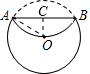
∵OA=4cm，
∴OC=2cm，
∴AC=2

3

cm，
∴AB=4

3

cm，
故答案为：4

3

．

点评：本题考查了勾股定理和垂径定理，解答这类题一些学生不会综合运用所学知识解答问题，不知从何处入手造成错解．