Question

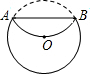
如图，将半径为4cm的圆形纸片折叠后，弧AB恰好经过圆心O，求折痕

AB

的长．

Answer 1

分析：连接OA，OB，过点O作OD⊥AB，根据折叠得到OD=2，由OA=4，再得出∠AOD的度数，进而得出

AB

的长．

解答：解：如图：连接OA，OB，过点O作OD⊥AB，
∵OA=4，

AB

是翻折后得到的，且恰好经过圆心O，
∴OD=2，
在Rt△OAD中，
∵OA=4，OD=2，
∴cos∠AOD=

1

2

∴∠AOD=60°，
∴∠AOB=120°，
∴

AB

=

120π×4

180

=

8

3

π．

点评：此题主要考查了垂径定理以及翻折的性质以及勾股定理等知识，根据已知得出∠AOD=60°是解题关键．