题目内容
2、Rt△ABC中,∠ACB=90°,CD⊥AB于D,DE⊥AC于E,那么和△ABC相似但不全等的三角形共有( )
分析:根据已知及相似三角形的判定,全等三角形的判定方法对其进行分析从而得到答案.
解答: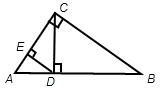 解:∵∠ACB=90°,CD⊥AB,DE⊥AC
解:∵∠ACB=90°,CD⊥AB,DE⊥AC
∴∠ACB=∠ADC=∠CDB=∠AED=∠DEC=90°
∵∠A=∠A,∠B=∠B,∠ACD=∠DCE
∴△ADC∽△CDB∽△ACB∽△AED,△ACD∽△DCE
∴△DCE∽△ABC
∴共有4个和△ABC相似但不全等的三角形
故选D
 解:∵∠ACB=90°,CD⊥AB,DE⊥AC
解:∵∠ACB=90°,CD⊥AB,DE⊥AC∴∠ACB=∠ADC=∠CDB=∠AED=∠DEC=90°
∵∠A=∠A,∠B=∠B,∠ACD=∠DCE
∴△ADC∽△CDB∽△ACB∽△AED,△ACD∽△DCE
∴△DCE∽△ABC
∴共有4个和△ABC相似但不全等的三角形
故选D
点评:此题考查了相似三角形的判定:
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.
①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;
③如果两个三角形的两个对应角相等,那么这两个三角形相似.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
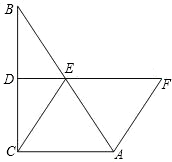 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形. 如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=
如图,在Rt△ABC中,∠BAC=90°,点D、E、F分别是三边的中点,且CF=3cm,则DE=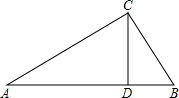 如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=
如图,Rt△ABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=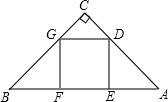 点G在边BC上.
点G在边BC上. 如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为
如图,Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AB,AB=20,AC=12,则四边形ADEC的面积为