题目内容
【题目】小明家今年种植的草莓喜获丰收,采摘上市20天全部销售完,爸爸让他对今年的销售情况进行跟踪记录,小明利用所学的数学知识将记录情况绘成图象(所得图象均为线段),日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,草莓的销售价p(单位:元/千克)与上市时间x(单位:天)的函数关系如图2所示设第x天的日销售额为w(单位:元)
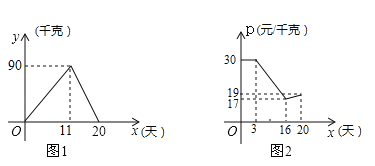
(1)第11天的日销售额w为 元;
(2)观察图象,求当16≤x≤20时,日销售额w与上市时间x之间的函数关系式及w的最大值;
(3)若上市第15天时,爸爸把当天能销售的草莓批发给了邻居马叔叔,批发价为每千克15元,马叔叔到市场按照当日的销售价p元千克将批发来的草莓全部售完,他在销售的过程中,草莓总质量损耗了2%.那么,马叔叔支付完来回车费20元后,当天能赚到多少元?
【答案】(1)1980;(2)w=﹣5(x﹣1)2+180, w有最大值是680元;(3)112元
【解析】
(1)当3≤x<16时,设p与x的关系式为p=kx+b,当x=11时,代入解析式求出p的值,由销售金额=单价×数量就可以求出结论;
(2)根据两个图象求得两个一次函数解析式,进而根据销售问题的等量关系列出二次函数解析式即可;
(3)当x=15时代入(2)的解析式求出p的值,再当x=15时代入(1)的解析式求出y的值,再由利润=销售总额进价总额车费就可以得出结论.
解:(1)当3≤x≤16时设p与x之间的函数关系式为p=kx+b
依题意得把(3,30),(16,17)代入,
![]() 解得
解得![]()
∴p=﹣x+33
当x=11时,p=22
所以90×22=1980
答:第11天的日销售额w为1980元.
故答案为1980;
(2)当11≤x≤20时设y与x之间的函数关系式为y=k1x+b1,
依题意得把(20,0),(11,90)代入得
解得
∴y=﹣10x+200
当16≤x≤20时设p与x之间的函数关系式为:p=k2x+b2
依题意得,把(16,17),(20,19)代入得

解得k2=![]() ,b2=9:
,b2=9:
∴p=![]() x+9
x+9
w=py=(![]() x+9)(﹣10x+200)
x+9)(﹣10x+200)
=﹣5(x﹣1)2+1805
∴当16≤x≤20时,w随x的增大而减小
∴当x=16时,w有最大值是680元.
(3)由(1)得当3≤x≤16时,p=﹣x+33
当x=15时,p=﹣15+33=18元,
y=﹣10×15+200=50千克
利润为:50(1﹣2%)×18﹣50×15﹣20=112元
答:当天能赚到112元.

 名校课堂系列答案
名校课堂系列答案