题目内容
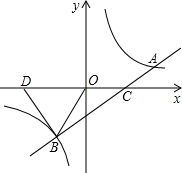
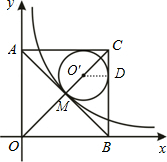
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=
经过正方形AOBC对角线的支点,半径为(4-2
)的圆内切于△ABC,求k的值.

| k |
| x |
| 2 |

设对角线的交点为M,内切圆的圆心为O',过O'作O'D⊥BC于D点,则O′D=4-2
,
在Rt△O'DC中,∠O'CD=45°,则sin∠O′CD=
,
即
=
∴O′C=4
-4,
∴CM=O′M+O′C=4-2
-4
-4=2
,
∴OM=2
,
∴点M坐标为(2,2),
∴y=
过M(2,2),
∴k=4.
| 2 |
在Rt△O'DC中,∠O'CD=45°,则sin∠O′CD=
| O′D |
| O′C |
即
| O′D |
| O′C |
| ||
| 2 |
∴O′C=4
| 2 |
∴CM=O′M+O′C=4-2
| 2 |
| 2 |
| 2 |
∴OM=2
| 2 |
∴点M坐标为(2,2),
∴y=
| k |
| x |
∴k=4.


练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
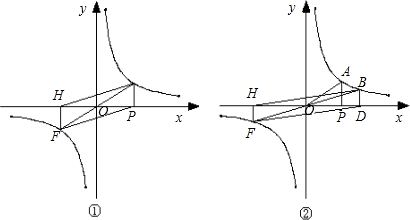
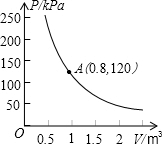
 间的函数关系如图所示,请根据图象提供的信息回答问题:
间的函数关系如图所示,请根据图象提供的信息回答问题: