题目内容
等腰三角形腰长为2cm,面积为1cm,则这个等腰三角形的顶角的余弦值为
或-
或-
.
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
分析:BD为腰AC上的高,根据三角形的面积公式得到S△ABC=
AC•BD,即
×2×BD=1,求得BD=1,然后根据勾股定理计算出AD,分类讨论:当△ABC为锐角三角形和钝角三角形,根据余弦的定义即可得到等腰三角形的顶角的余弦值.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:BD为腰AC上的高,
当△ABC为锐角三角形,如图,
AB=AC=2cm,
∴S△ABC=
AC•BD,即
×2×BD=1,
∴BD=1,
∴AD=
=
=
,
∴cos∠BAC=
=
.
当△ABC为钝角三角形,如图,
∴cos∠BAC=cos(180°-∠BAD)=-cos∠BAD=-
=-
.
故答案为
或-
.

当△ABC为锐角三角形,如图,
AB=AC=2cm,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=1,
∴AD=
| AB 2-BD2 |
| 22-12 |
| 3 |
∴cos∠BAC=
| AD |
| AB |
| ||
| 2 |
当△ABC为钝角三角形,如图,

∴cos∠BAC=cos(180°-∠BAD)=-cos∠BAD=-
| BD |
| AB |
| ||
| 2 |
故答案为
| ||
| 2 |
| ||
| 2 |
点评:本题考查了解直角三角形:利用锐角三角函数和勾股定理求出直角三角形形中未知的边与角叫解直角三角形.也考查了等腰三角形的性质.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目





 ,周长为
,周长为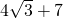 ,那么这个等腰三角形的腰长为
,那么这个等腰三角形的腰长为
 ,则腰长为( )
,则腰长为( )