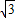题目内容
（1998•宁波）等腰三角形的底角为30°，底边长为2
，则腰长为（ ）
【答案】分析：作出底边上的高，根据等腰三角形的性质，在直角三角形中，根据底角的余弦求出腰长．
解答：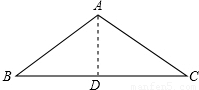
解：作AD⊥BC于D点．
∵△ABC是等腰三角形，AD⊥BC，∠B=30°，
∴BD=CD=
BC=
×2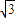
=
．
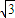∵cos∠B=cos30°=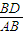
=
=
，
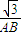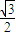∴AB=2．
故选C．
点评：本题很简单，根据等腰三角形的性质及特殊角的三角函数值解答．
解答：
解：作AD⊥BC于D点．∵△ABC是等腰三角形，AD⊥BC，∠B=30°，
∴BD=CD=
BC=×2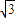=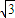．∵cos∠B=cos30°=
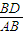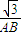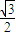==，∴AB=2．
故选C．
点评：本题很简单，根据等腰三角形的性质及特殊角的三角函数值解答．
练习册系列答案
相关题目
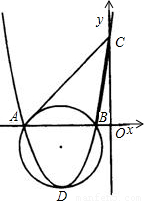
，二次函数y=ax2+bx+c图象经过A、B、C三点．
，二次函数y=ax2+bx+c图象经过A、B、C三点．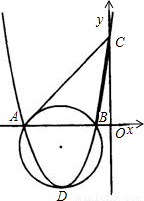
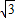，则腰长为（ ）
