题目内容
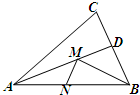 (2013•惠山区一模)如图,在锐角△ABC中,AB=6
(2013•惠山区一模)如图,在锐角△ABC中,AB=6| 2 |
6
6
.分析:从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.
解答:解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,
则BM′+M′N′为所求的最小值.
因为∠BAC的平分线交BC于点D,
由角平分线性质可知,M′H=M′N′,
当BH是点B到直线AC的距离时(垂线段最短),
∵AB=6
,∠BAC=45°,
∴BH=AB•sin45°=6,
所以BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=6.
故答案为6.
则BM′+M′N′为所求的最小值.
因为∠BAC的平分线交BC于点D,

由角平分线性质可知,M′H=M′N′,
当BH是点B到直线AC的距离时(垂线段最短),
∵AB=6
| 2 |
∴BH=AB•sin45°=6,
所以BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=6.
故答案为6.
点评:本题考查了轴对称的应用.易错易混点:解此题是受角平分线启发,能够通过构造全等三角形,把BM+MN进行转化,但是转化后没有办法把两个线段的和的最小值转化为点到直线的距离而导致错误.规律与趋势:构造法是初中解题中常用的一种方法,对于最值的求解是初中考查的重点也是难点.

练习册系列答案
相关题目
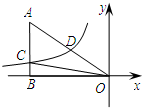 (2013•惠山区一模)如图,已知双曲线
(2013•惠山区一模)如图,已知双曲线