题目内容
【题目】解方程组
(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) 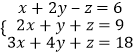
【答案】试题解析:(Ⅰ) ![]() ,
,
①×4得,4x+8y=60③,
③②得,5y=30,
解得y=6,
把y=6代入①得x=3,
∴方程组的解为 ![]() ;
;
(Ⅱ) 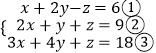 ,
,
①+②,得x+y=5④,
①+③,得2x+3y=12⑤,
⑤④×2,得y=2,
把y=2代入④,得x=3,
把x=3,y=2代入①,得z=1,
∴原方程组的解是 ![]() .
.
【解析】(Ⅰ)利用加减消元法解方程即可;(Ⅱ)第一个方程分别与第二、三个方程相加,消去z得到关于x与y的二元一次方程组,求出方程组的解得到x与y的值进而确定出z的值,得到方程组的解.
【考点精析】利用解二元一次方程组对题目进行判断即可得到答案,需要熟知二元一次方程组:①代入消元法;②加减消元法.

练习册系列答案
相关题目
【题目】某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如下表:
到超市的路程(千米) | 运费(元/斤·千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
设从甲养殖场调运鸡蛋x斤,总运费为W元
(1)试写出W与x的函数关系式.
(2)怎样安排调运方案才能使每天的总运费最省?