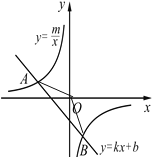
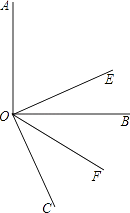
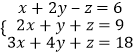��Ŀ����
����Ŀ������֪�����ڵ���ֱ�������κͺ���30���ǵ�ֱ���������У�����֮��ı�����ϵ�ֱ���ͼ��ʾ��
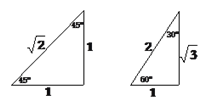
�Խ����������ۣ�����ͼ�Σ������������⣺
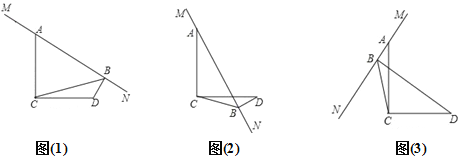
��ͼ(1)����֪��ACD=90����MN�ǹ���A��ֱ�ߣ�AC=DC��DB��MN�ڵ�B��
(1) ��֤�� BD+AB=![]() CB��
CB��
(2) ��MN��A��ת����ͼ(2)��ͼ(3)����λ��ʱ��BD��AB��CB����ʲô����ϵʽ����д����IJ��룬����ͼ(3)����֤����
(3) MN���Ƶ�A��ת�����У�����BCD=30����BD=![]() ʱ����CD=�� ����CB=�� ����
ʱ����CD=�� ����CB=�� ����
���𰸡���1��֤����������(2) ![]() ;
; ![]() ��(3)2��
��(3)2�� ![]() .
.
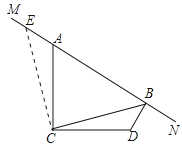
�������������������1������C��CE��CB�ڵ�C����MN���ڵ�E��֤����ACE�ա�DCB������ECBΪ����ֱ�������Σ��ݴ˼��ɵõ�BE=![]() CB������BE=AE+AB����֤�ã�
CB������BE=AE+AB����֤�ã�
��2������C��CE��CB�ڵ�C����MN���ڵ�E��֤����ACE�ա�DCB������ECBΪ����ֱ�������Σ��ݴ˼��ɵõ�BE=![]() CB������BE=AB-AE����֤�ã�
CB������BE=AB-AE����֤�ã�
��3������B��BH��CD�ڵ�H��֤����BDH�ǵ���ֱ�������Σ����DH�ij�����ֱ����BCH�У�����ֱ����������30����������Ե�ֱ�DZߵ���б�ߵ�һ�룬������ã�
�����������1������C��CE��CB�ڵ�C����MN���ڵ�E��
�ߡ�ACB+��BCD=90��,��ACB+��ACE=90����
���BCD=��ACE.
���ı���ACDB�ڽǺ�Ϊ360��,
���BDC+��CAB=180��.
�ߡ�EAC+��CAB=180����
���EAC=��BDC.
�֡�AC=DC,
����ACE����DCB,
��AE=DB,CE=CB,
����ECBΪ����ֱ��������,
��BE=![]() CB.
CB.
�֡�BE=AE+AB,
��BE=BD+AB,
��BD+AB=![]() CB��
CB��
(2)��ͼ(2) ABBD=![]() CB.�������£�
CB.�������£�

����C��CE��CB�ڵ�C����MN���ڵ�E��
�ߡ�ACD=90����
���ACE=90����DCE,��BCD=90����ECD��
���BCD=��ACE.
��DB��MN��
���CAE=90����AFC,��D=90����BFD��
�ߡ�AFC=��BFD��
���CAE=��D��
����ACE����DCB��, 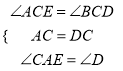 ��
��
����ACE����DCB(ASA)��
��AE=DB��CE=CB��
����ECBΪ����ֱ�������Σ�
��BE=![]() CB.
CB.
�֡�BE=ABAE��
��BE=ABBD��
��ABBD=![]() CB.
CB.
��ͼ(3):BDAB=![]() CB.�������£�
CB.�������£�
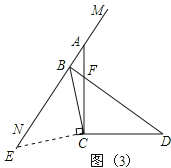
����C��CE��CB�ڵ�C����MN���ڵ�E��
�ߡ�ACD=90����
���ACE=90��+��ACB,��BCD=90��+��ACB��
���BCD=��ACE.
��DB��MN��
���CAE=90����AFB,��D=90����CFD��
�ߡ�AFB=��CFD��
���CAE=��D��
�֡�AC=DC��
����ACE����DCB��
��AE=DB��CE=CB��
����ECBΪ����ֱ�������Σ�
��BE=![]() CB.
CB.
�֡�BE=AEAB,
��BE=BDAB��
��BDAB=![]() CB.
CB.
(3)MN���Ƶ�A��ת�����У��������˼��û��ָ�������������
���ۺ��˵�һ��ͼ�͵ڶ���ͼ���������
���ǵ�1��ͼ��
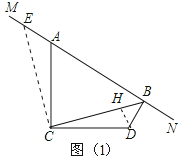
��(1)���ACE����DCB��CE=CB��
����ECBΪ����ֱ�������Σ�
���AEC=45��=��CBD��
��D��DH��CB.����DHBΪ����ֱ�������Ρ�
BD=![]() BH,
BH,
��BH=DH=1.
ֱ����CDH��,��DCH=30����
��CD=2DH=2,CH=![]() .
.
��CB=![]() +1��
+1��
���ǵڶ���ͼ����D��DH��CB��CB�ӳ�����H.
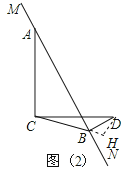
�ⷨ��������,CD=2,�ó�CB=![]() 1��
1��
�ʴ�Ϊ��2, ![]() +1��
+1��![]() 1.
1.