题目内容
已知:如图,在△ABC中,AD平分∠BAC,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)当AB≠AC时,猜想四边形ADCE形状,并加以证明;
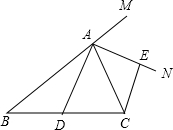
(2)如图,若添加“AB=AC”,其他条件不变,求证:四边形ADCE为矩形;
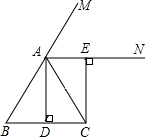
(3)在(2)的条件下,当△ABC满足什么条件时,四边形ADCE是一个正方形?(只需写出条件,不需证明)
解:(1)当AB≠AC时,四边形ADCE为直角梯形,
证明:∵AD平分∠BAC,AN是△ABC外角∠CAM的平分线,
∴∠DAC+∠CAE=90°,即∠DAE=90°
∵CE⊥AN,∴∠CEN=∠CEA=90°
∴∠DAE=∠CEN,∴AD∥EC,∵AD∥EC,AD≠CE,所以四边形ADCE为梯形,
又∠DAE=90°,所以是直角梯形.
(2)∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠ADC=90°,
由(1)可知,∠DAE=∠CEA=90°
∴四边形ADCE为矩形.
(3)例如,当AD= BC时,当∠BAC=90°时,当∠BCA=45°时,四边形ADCE均为正方形.
BC时,当∠BAC=90°时,当∠BCA=45°时,四边形ADCE均为正方形.
分析:(1)由题意可知,∠DAE=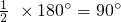 ,即DA⊥AN,又CE⊥AN,但AN与BC关系不确定,只能判断其为两个角是直角的四边形,则第一问可解;
,即DA⊥AN,又CE⊥AN,但AN与BC关系不确定,只能判断其为两个角是直角的四边形,则第一问可解;
(2)增加AB=AC后可判断AN∥BC,故由(1)可知其为矩形;
(3)在矩形的基础上,再加上一组邻边相等就行,例如△ABC为等腰直角三角形.
点评:猜想要在一定的理论基础上进行,不可盲目胡乱猜想,另外要熟练掌握矩形的性质及判定定理.
证明:∵AD平分∠BAC,AN是△ABC外角∠CAM的平分线,
∴∠DAC+∠CAE=90°,即∠DAE=90°
∵CE⊥AN,∴∠CEN=∠CEA=90°
∴∠DAE=∠CEN,∴AD∥EC,∵AD∥EC,AD≠CE,所以四边形ADCE为梯形,
又∠DAE=90°,所以是直角梯形.
(2)∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠ADC=90°,
由(1)可知,∠DAE=∠CEA=90°
∴四边形ADCE为矩形.
(3)例如,当AD=
 BC时,当∠BAC=90°时,当∠BCA=45°时,四边形ADCE均为正方形.
BC时,当∠BAC=90°时,当∠BCA=45°时,四边形ADCE均为正方形.分析:(1)由题意可知,∠DAE=
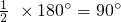 ,即DA⊥AN,又CE⊥AN,但AN与BC关系不确定,只能判断其为两个角是直角的四边形,则第一问可解;
,即DA⊥AN,又CE⊥AN,但AN与BC关系不确定,只能判断其为两个角是直角的四边形,则第一问可解;(2)增加AB=AC后可判断AN∥BC,故由(1)可知其为矩形;
(3)在矩形的基础上,再加上一组邻边相等就行,例如△ABC为等腰直角三角形.
点评:猜想要在一定的理论基础上进行,不可盲目胡乱猜想,另外要熟练掌握矩形的性质及判定定理.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,