题目内容
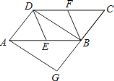
【题目】如图,在等腰![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向运动,同时点
方向运动,同时点![]() 从
从![]() 出发,以相同的速度沿射线
出发,以相同的速度沿射线![]() 方向运动,连
方向运动,连![]() ,交直线
,交直线![]() 于点
于点![]()
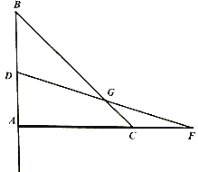
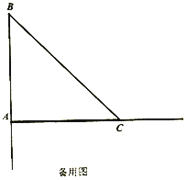
![]() 当点
当点![]() 运动到
运动到![]() 中点时,求
中点时,求![]() 的长.
的长.
![]() 求证:
求证:![]() .
.
![]() 过点
过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() ,请探究
,请探究![]() 之间的数量关系,并直接写出结论.
之间的数量关系,并直接写出结论.
【答案】(1)![]() ;(2)证明见解析;(3)当点
;(2)证明见解析;(3)当点![]() 在
在![]() 上时,
上时,![]() ;当点
;当点![]() 在
在![]() 的延长线上时
的延长线上时![]()
【解析】
(1)根据题意得出CF,然后利用勾股定理即可得出DF;
(2)首先作![]() ,利用平行的性质构造
,利用平行的性质构造![]() ,即可得证;
,即可得证;
(3)分情况探究:当点![]() 在
在![]() 上和
上和![]() 的延长线上时,利用三线合一的性质进行等量转换即可.
的延长线上时,利用三线合一的性质进行等量转换即可.
(1)由题意,得AD=CF=![]() =2,
=2,
∴AF=AC+CF=4+2=6
∴![]()
(2)作![]() ,如图所示:
,如图所示:
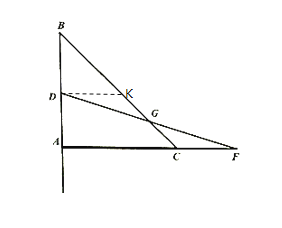
∴∠BKD=∠BCA,∠KDG=∠CFG
∴∠DKG=∠FCG
∵D为AB中点,DK∥AC
∴DK=CF
∴![]() (ASA),
(ASA),
∴![]()
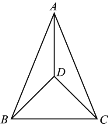
(3)当点![]() 在
在![]() 上时,如图所示,
上时,如图所示,
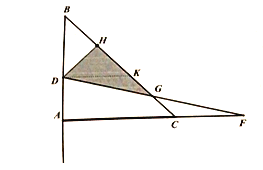
∵等腰![]()
∴∠B=45°
∵![]()
∴BH=HK
∵![]()
∴KG=CG
∴![]() ;
;
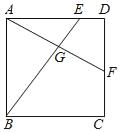
当点![]() 在
在![]() 的延长线上时,如图所示:
的延长线上时,如图所示:
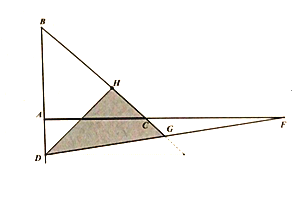
∵等腰![]()
∴∠B=45°
∵![]()
∴BH=GH
∴![]()

练习册系列答案
相关题目
【题目】某数学兴趣小组在本校九年级学生中以“你最喜欢的项体育运动"为主体进行了抽样调查,并将调查结果绘制成下表和下图.
项目 | 篮球 | 乒乓球 | 羽毛球 | 跳绳 | 其他 |
人数 |
| 12 | 10 | 5 | 8 |

请根据图表中的信息完成下列各题:
(1)本次共调查学生______名;
(2)![]() =______;
=______;
(3)在扇形图中,“跳绳”对应的扇形圆是______.