题目内容
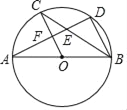
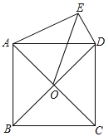
【题目】如图,在⊙O中,D、E分别是半径OA、OB的中点,C是![]() 上一点,CD=CE.
上一点,CD=CE.
(1)求证:![]() =
=![]() ;
;
(2)若∠AOB=120°,CD=![]() ,求半径OA的长.
,求半径OA的长.

【答案】(1)证明见解析;(2)OA=2;
【解析】
(1)连接OC、AC,由D、E分别是半径OA、OB的中点求出OD=OE,根据CD=CE,OC=OC可证明△OCD≌△OCE,进而证明∠AOC=∠COB,即可证明![]() .(2)根据∠AOC=∠COB,可知∠COD=60°,进而可知△AOC是等边三角形,根据CD是中线,可证明CD⊥AD,在Rt△OCD中根据利用勾股定理求出OC的长即可.
.(2)根据∠AOC=∠COB,可知∠COD=60°,进而可知△AOC是等边三角形,根据CD是中线,可证明CD⊥AD,在Rt△OCD中根据利用勾股定理求出OC的长即可.
(1)连接OC,
∵D、E分别是半径OA、OB的中点,
∴OD=OE,
∵OC=OC,CD=CE,OD=OE,
∴△OCD≌△OCE,
∴∠AOC=∠COB,
∴![]()
(2)∵∠AOB=120°,∠AOC=∠COB,
∴∠AOC=60°,
∴△AOC是等边三角形,
∵CD是中线,
∴CD⊥AD,∠OCD=30°,
∴OD=![]() OC,
OC,
∴OC2=![]() OC2+(
OC2+(![]() )2
)2
解得:OA=OC=2.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目