题目内容
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
【答案】
(1)证明:
如图1,连接OD,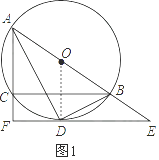
∵EF是⊙O的切线,且点D在⊙O上,
∴OD⊥EF,
∵OA=OD,
∴∠DAB=∠ADO,
∵AD平分∠BAC,
∴∠DAB=∠DAC,
∴∠ADO=∠DAC,
∴AF∥OD,
∴AF⊥EF
(2)解:
如图2,过D作DG⊥AE于点G,连接CD,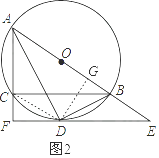
∵∠BAD=∠DAF,AF⊥EF,DG⊥AE,
∴BD=CD,DG=DF,
在Rt△ADF和Rt△ADG中![]()
∴Rt△ADF≌Rt△ADG(HL),
同理可得Rt△CDF≌Rt△BDG,
∴BG=CF=2,AG=AF=AC+CF=6+2=8,
∴AB=AG+BG=8+2=10,
∴⊙O的半径OA= ![]() AB=5
AB=5
【解析】(1)如图1,连接OD,根据圆的切线垂直于经过切点的半径可得OD⊥EF,由AD平分∠BAC可得∠DAB=∠DAC,结合已知可得∠ADO=∠DAC,用平行线的性质可得AF∥OD,所以AF⊥EF。
(2)如图2,过D作DG⊥AE于点G,连接CD,根据斜边直角边定理可证Rt△ADF≌Rt△ADG,Rt△CDF≌Rt△BDG,所以有BG=CF,AG=AF=AC+CF,则AB=AG+BG,⊙O的半径OA= ![]() AB.
AB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目