题目内容
【题目】如图,已知抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 之间的一个动点,过点
之间的一个动点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)若![]() 为
为![]() 的中点,求
的中点,求![]() 的长;
的长;
(3)如图,以![]() ,
,![]() 为边构造矩形
为边构造矩形![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,
,
①请求出![]() ,
,![]() 之间的关系式;②求出矩形
之间的关系式;②求出矩形![]() 的周长最大时,点
的周长最大时,点![]() 的坐标.
的坐标.
【答案】(1)y=x2+2x;(2)![]() ;(3)①
;(3)①![]() ;②P(0,0)
;②P(0,0)
【解析】
(1)把A点坐标代入直线方程可求得a的值,再代入抛物线可求得b的值,可求得抛物线解析式;
(2)联立抛物线和直线解析式可求得B点坐标,过A作AQ⊥x轴,交x轴于点Q,可知OC=![]() AQ=4,可求得C点坐标,结合条件可知P点纵坐标,代入抛物线解析式可求得P点坐标,从而可求得PC的长;
AQ=4,可求得C点坐标,结合条件可知P点纵坐标,代入抛物线解析式可求得P点坐标,从而可求得PC的长;
(3)①根据矩形的性质可分别用m、n表示出C、P的坐标,根据DE=CP,可得到m、n的关系式.
②根据①中可得DE和CD,以及![]() 、
、![]() 之间的关系式可用n表示m,代入
之间的关系式可用n表示m,代入
解:(1)∵A(a,8)是抛物线和直线的交点,
∴A点在直线上,
∴8=2a+4,解得a=2,
∴A点坐标为(2,8),
又A点在抛物线上,
∴8=22+2b,解得b=2,
∴抛物线解析式为y=x2+2x;
(2)联立抛物线和直线解析式可得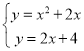 ,
,
解得![]() ,
,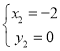 ,
,
∴B点坐标为(-2,0),
如图,过A作AQ⊥x轴,交x轴于点Q,
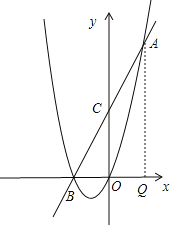
则AQ=8,OQ=OB=2,即O为BQ的中点,
当C为AB中点时,则OC为△ABQ的中位线,即C点在y轴上,
∴OC=![]() AQ=4,
AQ=4,
![]() 点坐标为
点坐标为![]() ,
,
又![]() 轴,
轴,
![]() 点纵坐标为4,
点纵坐标为4,
![]() 点在抛物线上,
点在抛物线上,
![]() ,解得
,解得![]() 或
或![]() ,
,
![]() 点在
点在![]() 、
、![]() 之间的抛物线上,
之间的抛物线上,
![]() 不合题意,舍去,
不合题意,舍去,
![]() 点坐标为
点坐标为![]() ,
,![]() ,
,
![]() ;
;
(3)①![]() ,且四边形
,且四边形![]() 为矩形,
为矩形,
![]() 点横坐标为
点横坐标为![]() ,
,![]() 点纵坐标为
点纵坐标为![]() ,
,
![]() 、
、![]() 都在直线
都在直线![]() 上,
上,
![]() ,
,![]() ,
,![]() ,
,
![]() 轴,
轴,
![]() 点纵坐标为
点纵坐标为![]() ,
,
![]() 点在抛物线上,
点在抛物线上,
![]() ,整理可得
,整理可得![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
![]() 点坐标为
点坐标为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,即
,即![]() ,
,
整理可得![]() ,
,
即![]() 、
、![]() 之间的关系式为
之间的关系式为![]() ;
;
②根据①中结论可知,![]() ,
,![]() ,
,
矩形PCDE的周长=![]()
=![]() ,
,
∵![]() ,
,
∴![]() ,代入,
,代入,
∴矩形PCDE的周长=![]() ,
,
当n=4,最大值为12,
可得m=-2,
此时点P坐标为(0,0).

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案【题目】学校开展的“书香校园”活动受到同学们的广泛关注,为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计图表.
学生借阅图书的次数统计表:
借阅图书的次数 |
|
|
|
|
|
人数 |
|
|
|
|
|

请你根据统计图表中的信息,解答下列问题:
(1)![]() ,
,![]() ;
;
(2)该调查统计数据的中位数是 ,众数是 ;
(3)若该校共有![]() 名学生,根据调查结果,估计该校学生在一周内借阅图书
名学生,根据调查结果,估计该校学生在一周内借阅图书![]() 次及以上的人数.
次及以上的人数.