题目内容
 (2012•大兴区二模)已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
(2012•大兴区二模)已知二次函数y=ax2+bx+2,它的图象经过点(1,2).(1)如果用含a的代数式表示b,那么b=
-a
-a
;(2)如图所示,如果该图象与x轴的一个交点为(-1,0).
①求二次函数的表达式,并写出图象的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图象上所有等距点的坐标.
(3)当a取a1,a2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小.
分析:(1)直接将点(1,2)代入抛物线的解析式中,即可得到a、b间的关系式.
(2)①已知抛物线图象上的两点坐标,且只有两个待定系数,利用待定系数法求解即可.
②P到x轴、y轴的距离相等,那么P点必在直线y=x或y=-x上,这两条直线与抛物线的交点,即为符合条件的等距点.
(3)首先根据(1)的结论,用a表示出函数的解析式,然后分别将M、N的坐标代入抛物线的解析式中,分别用m、n表示出a1、a2,通过做差可比较出a1、a2的大小.
(2)①已知抛物线图象上的两点坐标,且只有两个待定系数,利用待定系数法求解即可.
②P到x轴、y轴的距离相等,那么P点必在直线y=x或y=-x上,这两条直线与抛物线的交点,即为符合条件的等距点.
(3)首先根据(1)的结论,用a表示出函数的解析式,然后分别将M、N的坐标代入抛物线的解析式中,分别用m、n表示出a1、a2,通过做差可比较出a1、a2的大小.
解答:解:(1)将(1,2)代入y=ax2+bx+2中,得:
a+b+2=2,得:b=-a.
(2)①∵二次函数y=ax2+bx+c经过点(1,2)和(-1,0)
可得
,
解得
,
即y=-x2+x+2,
顶点坐标为(
,
).
②该函数图象上等距点的坐标即为此函数与函数y1=x和函数y2=-x的交点坐标
,
,
解得P1(
,
)、P2(-
,-
)、P3(1+
,-1-
)、P4(1-
,
-1).
(3)∵二次函数与x轴正半轴交于点(m,0)且a=-b,
∴a1m2-a1m+2=0,即 a1=
,
同理 a2n2-a2n+2=0,a2=
,
故 a2-a1=
-
=
,
∵n>m>1,故 a2-a1=
>0,
∴a1<a2.
a+b+2=2,得:b=-a.
(2)①∵二次函数y=ax2+bx+c经过点(1,2)和(-1,0)
可得
|
解得
|
即y=-x2+x+2,
顶点坐标为(
| 1 |
| 2 |
| 9 |
| 4 |
②该函数图象上等距点的坐标即为此函数与函数y1=x和函数y2=-x的交点坐标
|
|
解得P1(
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
(3)∵二次函数与x轴正半轴交于点(m,0)且a=-b,
∴a1m2-a1m+2=0,即 a1=
| 2 |
| m-m2 |
同理 a2n2-a2n+2=0,a2=
| 2 |
| n-n2 |
故 a2-a1=
| 2 |
| n-n2 |
| 2 |
| m-m2 |
| 2(m-n)(1-m-n) |
| mn(1-m)(1-n) |
∵n>m>1,故 a2-a1=
| 2(m-n)(1-m-n) |
| mn(1-m)(1-n) |
∴a1<a2.
点评:该题考查了二次函数解析式的确定、函数图象交点坐标的求法以及不等式的应用等知识,综合性较强,属于基础知识的综合考查,难度适中.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
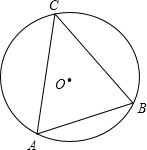 (2012•大兴区二模)如图,⊙O的半径为6,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是
(2012•大兴区二模)如图,⊙O的半径为6,点A、B、C在⊙O上,且∠ACB=45°,则弦AB的长是